参考文献

第十八章　恒值粉碎机解法

印度库达卡的源流是当今世界数学史上的难点，众说纷纭，莫衷一是。

降系数不定方程的取解式基于现代辗转法，依附于余数0。婆罗摩笈多恒值粉碎机的原术、原意，取解式基于原始辗转相除法，依附于余数1的整除式。

18.1　库达卡史料

阿耶波多一世是迄今所知最早的印度数学家。公元499年著有《圣使文集》凡四章，十节诗、数学、时间计算和天球。其中数学章由三十三节组成，最后两节为押韵诗句，自称库达卡（Kuttaka）。此书长期失传，直到1864年印度学者勃豪·丹吉才获得抄本。

阿耶波多一世一生中对纯数学最大的贡献是库达卡，其立术成为印度传统数学重要组成部分。《圣使文集》有关库达卡的原文如图18.1：

图18.1　库塔卡影印资料

这些片言只语经门生婆什迦罗一世（Bháscara I）解释，再经后人补充，其义始显。

印度数学史家达生[1]（Datta，Bibhutibhusan，1888—1958），出生于贫穷家庭，终生未婚，对于世间的乐趣毫无兴趣。他的博士论文研究流体动力学，他却以数学史研究而闻名于世。

达生[2]根据婆什迦罗一世的解释，用近代通用数学语言进行了解释。

达生和辛格（Singh，A.N.）在《印度数学史》[3]中进一步解释为：

相应于较大余数的除数被相应于较小余数的除数除，所得余数又与相应于较小余数的除数除。自下乘上面一个，加下面一个。

意思是：求一数N，以两个给定数a，b除，留下两个余数R1，R2，即N=ax+R1=by+R2。以c作R1与R2之差，我们有：（ⅰ）by=ax+c，如果R1＞R2；（ⅱ）ax=by+c，如果R2＞R1。

《库达卡与大衍求一术》[4]（下面简称库文）一文中，解释上面译文：

32节对应于较大余数（R1）的除数（a）被对应于较小余数（R2）的除数（b）除，所得余数（r1）又与对应于较小余数的除数（b）除。[照此继续进行除法运算，余数渐小。其最后余数rm应乘一任择之数（t）使乘积加上（如商的序号m为奇），或减去（如商的序号m为偶）原来余数之差（R1-R2=c）适为倒数第二个余数（rm=1）所整除，记商为q。把互除所得各商数（q1，q2，…，qm）依次排成一列，再在其末尾添上所选定的乘数t，最后记上被倒数第二个余数整除的商q。]

33节 [在这一列数中]自下[倒数第二个]乘上面一个，加下面一个。[重复这一手续，用较大余数对应的除数（a）来除所得最后一数（y），其余数乘以较小余数所对应的除数（b）加上较小余数R2，结果就是对应于二除数的所求数（N）。]

库文还增添评注：“方括号内文字系后人补充、注释，可见圣使原文极为简陋，隐晦难晓。”

库文以不定方程137x+10=60y为例，演示库达卡。此题世称阿耶波多不定方程，是广泛收集于世界数学史各大名著中的典型数例。

18.2　降系数不定方程

18.2.1　降系数不定方程来源

达生、辛格按自然余数1商个数的奇偶，把整数对分成两大类。把两系数辗转相除到余数1、余数0，列为情况ⅰ。情况ⅱ，则指辗转相除中途结束，并未求到余数1、余数0。

降系数不定方程的字母体系与脚码繁复难记。为方便读者，我们以阿耶波多不定方程137x+10=60y为例，属于ax+c=by（I），附加数c紧随大系数ax。因137x+10=60y，两系数137和60辗转相除，自然余数r4=1的除法序数是4，为偶数。因此，137和60为偶序整数对。

依据欧拉变量代换基本思路，列出偶序整数对的降系数不定方程演算表（表18.1）。

表18.1　偶序整数对137与60降系数不定方程

第4次除法出现自然余数1（r4），引入新变量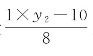，整理成降系数不定方程8x2+10=y2。

第5次除法为余数0，没有引入新变量，整理成8x2=1×y2-10，也是降系数不定方程。

下面，我们逐字翻译英文版[5]（2001年最新版）第86到99页，达生、辛格的降系数不定方程的解法。对核心段落情况（ⅰ.1），即偶序整数对且辗转相除到余数0的这一段，特地插入方括号的编号注释。

偶序整数对137和60辗转相除，余数为0时，商总个数5，奇数。第4次除法9=8×1+1得余数1，商个数4，为偶数。脚注中，记n=2，于是，2n=4，2n-1=3。

这里展示的降系数不定方程解法，属于1770年欧拉的“形式分数的分母值取1”方案的思路，不列作单独的解法。参见本书11.2.1“解法分类”。

我们发现，达生、辛格处理不慎，瑕疵不少。

译文“情况（ⅰ.1）设商个数为偶数”一条，“方程（I.2n）和（I.2n+1）就分别变成yn=q2nxn+c，而yn+1=c”中，yn=q2nxn+c就是个瑕疵，应为yn=q2nxn-c，即降系数不定方程为8x2=1×y2-10，y3=10。

后面的“q2n=r2n-1”为q4=r3，我们代入q4=1，r3=8，得到1=8，又是个瑕疵。

后面的“情况（ⅰ.2）设商个数为奇数……q2n-1=r2n-2”，为同样的错误。

假如R1＞R2，所解的不定方程是ax+c=by（I），这里，a，b互素。

这样，我们有[原注：当a＜b时，有q=0，r1=a]

a=bq+r1,

b=r1q1+r2,

r1=r2q2+r3,

r2=r3q3+r4,

…

rm-2=rm-1qm-1+rm,

rm-1=rmqm+rm+1。

[注1：商q脚码从数字0起，如y=qx+y1。库文用q1，相差1，不影响计算。依次类推。]

现在在方程（I）中代入a的值，有by=（bq+r1）x+c。因此，y=qx+y1，其中by1=r1x+c。

换句话说，因为a=bq+r1，置入y=qx+y1，方程（I）降低成by1=r1x+c（I.1）。

[注2：相当于把（I）137x=60y+10演化成为降系数不定方程60y1=17x+10（I.1）。]

同样，因b=r1q1+r2，类似地置入x=q1y1+x1，方程（I.1）进一步降低成r1x1=r2y1-c，等等。

[注3：相当于把（I.1）60y1=17x+10演化成为降系数不定方程17x1=9y1-10（I.2）。]

分列写出一系列的值和降系数不定方程，我们有

(1)y=qx+y1,　by1=r1x+c;　(I.1)

(2)x=q1y1+x1,　r1x1=r2y1-c;　(I.2)

(3)y1=q2x1+y2,　r2y2=r3x1+c;　(I.3)

(4)x1=q3y2+x2,　r3x2=r4y2-c;　(I.4)

…,　…;

(2n-1)yn-1=q2n-2xn-1+yn,　r2n-2yn=r2n-1xn-1+c;　(I.2n-1)

(2n)　xn-1=q2n-1yn+xn,　r2n-1xn=r2nyn-c;　(I.2n)

(2n+1)yn=q2nxn+yn+1,　r2nyn+1=r2n+1xn+c。　(I.2n+1)

[注4：降系数不定方程（I.4），r3x2=r4y2-c，常数c前是减号。这是正确的。]

于是辗转相除法能继续演算，或（ⅰ）到结束，或（ⅱ）得到一系列商，再终止。这两种情况下，所发现商的个数，忽略第一个（q），如同阿耶波多说，可以是奇的，可以是偶的。

[注5：相当于回代过程中，只求出不定方程的x值，省略求y值。不影响计算。]

情况（ⅰ） 首先假定辗转相除法能继续演算，直到余数零。因为a，b互素，倒数一个余数是单位1。

情况（ⅰ.1） 设商个数为偶数，我们有r2n=1，r2n+1=0，q2n=r2n-1。

[注6：辗转相除过程中，只有除数与被除数更替交换，事实上，不可能出现商q2n=余数r2n-1。]

方程（I.2n）和（I.2n+1）就分别变成yn=q2nxn+c，而yn+1=c。[注7：即方程（I.4）和（I.5）就分别变成y2=q4x2-10，而y3=10。误把常数前的减号变成加号，见注4。]赋予xn适当的整数值（t），我们得到yn的整值。[注8：赋予x2适当的整数值t，不妨说t=0。就得到y3=q=10，得到y3的整值。]就此，我们能从（2n）找到xn-1的值。一步步往回推算，最后求出x，y正整数值。从而解出方程（I）。

情况（ⅰ.2）设商个数奇数，我们有r2n-1=1，r2n=0，q2n-1=r2n-2。方程（2n+1）和（I.2n+1）可省略，方程（I.2n-1）和（I.2n）就分别降系数，变成xn-1=q2n-1yn-c，而xn=-c。

[注9：事实上，辗转相除过程中，不可能出现商q2n-1=余数r2n-2。]

赋予yn适当的整数值（t′），我们得到xn-1的整值。如前一步步往回推算，我们求出x，y整数值。

情况（ⅱ） 下面假定辗转相除法在得到一个奇的或偶的商个数之后，终止。

情况(ⅱ.1) 设商个数为偶数,原方程的降系数形式是r2nyn+1=r2n+1xn+c或。如赋予xn以适当的整数值t,使得是一个整数,据(2n+1)我们有yn的整值。如前,我们求出x,y的整数值。

情况(ⅱ.2)设商个数奇数,商[误。注10:原文就误作quotient]的降系数形式是r2n-1xn=q2nyn-c,或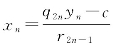。如赋予yn=t′,t′是整数,使得是一个整数。据(2n)我们找到xn-1的整值。故求出x,y整数值。

注意,情况(ⅰ)中求到余数0,肯定采用降系数不定方程,作为取解式。

情况(ⅱ)中,辗转相除不达到余数1、余数0,只是说商个数有偶数、有奇数,无法确定取解式。只说成是降系数不定方程r2nyn+1=r2n+1xn+c,或者是整除式

注意，情况（ⅰ）中求到余数0，肯定采用降系数不定方程，作为取解式。

情况（ⅱ）中，辗转相除不达到余数1、余数0，只是说商个数有偶数、有奇数，无法确定取解式。只说成是降系数不定方程r2nyn+1=r2n+1xn+c，或者是整除式。

我们更发现，依现代辗转相除为背景的降系数不定方程以余数0为背景，与原始辗转相除为背景的整除式混为一谈，就会犯错。恰巧，库文就提供了这样的典型。

18.2.2　混淆取解式

《库达卡与大衍求一术》[6]一文中，求解不定方程137x+10=60y，应用达生、辛格降系数不定方程的结论。文中所说“情况1.1.1”，就是达生、辛格的情况（ⅰ.1），设商个数为偶数，我们有r2n=1，r2n+1=0。

求解过程全录如下。

例1 137x+10=60y。

这里a=137，b=60，c=10，辗转相除得

q1=2,q2=3,q3=1,q4=1,q5=8,

r1=17,r2=9,r3=8,r4=1,r5=0。

从情况1.1.1，y2=q5t+10=8t+10，t可以随意选，如t=1=x2，得y2=18。

于是从下而上递推依次得回代过程是

y=q1x+y1=2×130+37=297,

x=q2y1+x1=3×37+19=130,

y1=q3x1+y2=1×19+18=37,

x1=q4y2+x2=1×18+1=19,

y2=18,

x2=1。

印度人氏习惯上把上面运算排成图式：

第一部分辗转相除和第三部分回代，不易犯错，关键在于取解式。

在本书18.3.3“用变量分析解137x+10=60y”中，我们分析了两种取解式。

自然余数取1，由新变量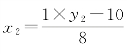，得整除式，有初解：取y2=18，则有x2=1。

余数为0，降系数不定方程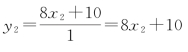中，有初解：取x2=1，则有y2=18。

库文中，用y2=q5t+10=8t+10，用到q5=8，余数r5=0，采用降系数不定方程取初解。我们看到，从“t可以随意选，如t=1=x2”，算得“y2=18”，明显不符合整除式取初解，即余数1初解的原术原意。见本书18.4“婆罗摩笈多的解法”。

18.3　基本解法试解

我们应用序列值解法和变量分析法，剖析阿耶波多不定方程解法的每一个可能细节。

18.3.1　序列值解法

根据《算术研究》第27节，用序列值解法处理137和60，求出不定方程137x+1=60y的一组特殊解x=7，y=16。再用137x+10=60y的一组特殊解。

高斯表述解的依赖性时，采用同余式：

观察形如ax+t≡u的同余式，这个同余式是依赖于ax≡±1的。

而同余式与不定方程等价：

不定方程ax=by±1与以b为模的同余式ax≡+1等价。

分三步解出阿耶波多不定方程：

（1）取137x+10=60y的两系数137和60，计算序列值（表18.2）。

表18.2　偶序整数对137与60序列值计算

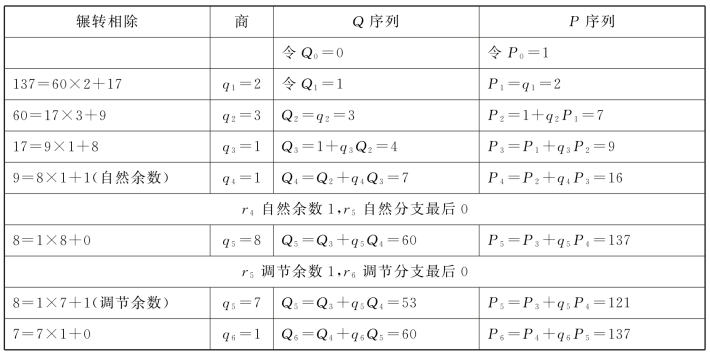
（2）两系数组成的整数对，因自然余数除法序数的奇、偶，分成两大类：奇序整数对和偶序整数对。每大类整数对又因商数损一调节举措，分两个余数分支，组合成四种并列的情况。高斯配置法则说：

当[α，β，γ，…，μ，n]项的个数是偶数时，我们有ax=by+1，当项的个数是奇数时，我们有ax=by-1。

因自然余数1的除法序数4为偶数，项的个数即商的总个数5为奇数，所以选取不定方程137x=60y-1，即137x+1=60y。

因自然余数1序列值是Q4=7，P4=16，所以x=7，y=16是常数1不定方程137x+1=60y的最小正整数解。核算：7×137=959=16×60-1。

（3）不定方程137x+10=60y的常数10是137x+1=60y常数1的10倍。

以x=7，y=16乘10，得x=70，y=160。

再各除以对方系数，得x=70÷60余10，y=160÷137余23，所以x=10，y=23是137x=60y-10的一组最小正整数解。核算：137×10=1370=23×60-10。

可见，x=10，y=23是不定方程137x+10=60y的一组特殊解。

18.3.2　变量分析法试解

前面，我们分析欧拉的整数解思想，列出表9.1和表11.1。我们在表格中添入方括号[添]字来表示的各项，扩展为降系数不定方程表（表18.3）。

先看列。第三列为商5，2，1。第五列引入的新变量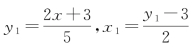，都是形式上的分数、实质上的整数。整理新变量得第六列，为降系数不定方程2x+3=5y1，y1-3=2x1。第六列的降系数不定方程2x=5y1-3，y1=2x1+3，演变成第一列。

再看行。第一行出现新变量y1，第二行出现x1。第三行y1=2×x1+3是降系数不定方程，没有新变量。

表18.3　5y=7x+3的降系数不定方程表

欧拉求的是通解。余数为0时，有y1=2x1+3。转入回代，得通解x=5x1+6，y=7x1+9，这里取x1作任意整数。

18.3.3　用变量分析解137x+10=60y

我们用欧拉的思路，试解137x+10=60y（表18.4）。两系数为偶序整数对，附加数10为正，恰巧与5y=7x+3是同一类型。

表18.4　137x+10=60y的变量分析表

续表

由此，我们看到两种取解式：自然余数1取解式和余数0取解式，背景不同。

表18.4中，8=1×8+0，余数为0时有降系数不定方程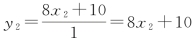。满足降系数不定方程的，先有初解x2=1，再有y2=18。

9=8×1+1，余数为1时，有新变量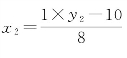。满足整除式，有初解y2=18，才有x2=1。

可见，依据原始辗转相除所取得的初解，只适应整除式，不适应现代辗转相除背景下的降系数不定方程。

18.4　婆罗摩笈多的解法

18.4.1　原术原意

婆罗摩笈多（Brahmegupta，梵藏，约598—约665），早期乌贾因（Ujain）学派代表，628年著有《婆罗摩修正体系》。655年完成另一本天文著作。

狄克逊英文版《数论史》所列史料，夹叙夹议，介绍婆罗摩笈多术文和数例二，讨论恒值粉碎机。所列文献原始信息抄录如下：Brahme-sphut'hánta，Ch.18（Cuttaca=algebra），Colebrooke，pp.330-331。

我们先录《数论史》英文，再全译如下：

Brahmegupta(born 598 A.D.)gave the following rule to find a constant“pulverizer”.From the given multiplier and divisor,remove their greatest common divisor(found by mutual division).The thus reduced multiplier and divisor are mutually divided until the residue unity is obtained,and the quotients are written in order.Multiply the residue unity by a number chosen so that the product less one(or plus one,if there be an odd number of quotients)shall be exactly divisible by the divisor which produced the residue unity.After the above listed quotients place this chosen number and after it the quotientjust obtained.To the ultimate add the product of the penultimate by the next preceding term[etc.].The number found,or its residue after division by the reduced divisor,is the constant pulverizer.

术文分成三段，我们依次编号。

婆罗摩笈多（梵藏）（生于公元598年）叙述了寻找恒值“粉碎机”的法则。（术文1）根据已知的乘数和除数，用（辗转相除法找到的）最大公约数，加以约简。如此约简后的乘数和除数辗转相除，直到余数单位1而止，并依次记下商值。（术文2）对余数单位1乘以一个所选择的数，使得乘积减去1（或者加上1，当商个数为奇数时），将可以由产生余数单位1的相应除数所整除。（术文3）在上列商值之下，放置这个所选定的数，此后再放置刚求得的商值。对于最后数，加上中间数与下一个前置项的乘积（等等）。所找到数，或其经约简除数的除法之后的余数，就是恒值粉碎机。

数例二讲述阿耶波多不定方程137x+10=60y。同样分成三段，依次标明。

Again(§27,p.336),let the reduced dividend[multiplier]and divisor be 137 and 60,while the augment or additive quantity is 10.By reciprocal division of 137 and 60,we get the quotients 0,2,3,1,1 and last two remainder 8 and 1.Since the augment is now positive and the number of quotients is odd and since 1·9-1 is divisible by 8,we select 9 as the chosen number.The constant pulverizer is said to be found as before.Its product by 10 is divided by 60 to give the desired multiplier 10;10·137+10=60·23.

又（§27，p.336），（数例二1）设约简的被除数[乘数]和除数为137和60，而增加或附加数为10。通过137和60辗转相除，我们得到商值0，2，3，1，1，最后两个余数是8和1。（数例二2）因为附加数现在为正，商个数为奇数[见下面的译者注]，又因为1×9-1可被8整除，我们选9作为选定数。（数例二3）据说可如前一样找到恒值粉碎机。它与10的乘积可被60除，以得到所需的乘数10；10×137+10=60×23。

我们知道137x+10=60y。两系数137和60辗转相除到余数1时的商个数4是偶数。增加了商为0的除法60=137×0+60，余数1的商个数从4增加到5，成了奇数。

这里要讨论一下术文“已知的乘数”、“如此约简后的乘数”、数例二题首“被除数[乘数]137”，都是指所求未知数x。题尾计算所得的“所需的乘数10”，即x=10，则是阿耶波多不定方程的解。印度数学史的注释中，公认库达卡解释为“乘数”[7]，记为x。可见，库达卡所指，似乎过于广泛。

1　单位1的关联

术文第一段，利用1构作整除式，需要两系数重复两次辗转相除，保证得到余数1。当然，还需要利用附加数非常数1的原不定方程，构作附加数1的不定方程。

单位1的作用、余数1与附加数1的关联早在6世纪时的婆罗摩笈多的恒值粉碎机解法中就体现出来了。

我们在18.3.1“序列值解法试解”中提到，1801年高斯的不定方程的序列值解法依靠解的依赖性。线性不定方程ax=by±1中，a，b是正整数，a不小于b。由可解条件，a与b互素，辗转相除，自然余数1，与附加数1相对应。求出不定方程ax=by±1的解，就可以解出一般常数的不定方程ax=by±c。

（数例二1）中说，“设约简的被除数[乘数]和除数为137和60，而增加或附加数为10”，我们采纳大系数ax约定，紧随附加数10，写成阿耶波多不定方程137x+10=60y。

第一次辗转相除，如（术文1）说，“根据已知的乘数和除数，用（辗转相除法找到的）最大公约数，加以约简”，可约得互素的系数。

再次辗转相除，互素两系数一定求出自然余数1。

根据原有方程137x+10=60y，进行默认的预处理，得到附加数1的137x+1=60y。

2　整除式的构作

由于缺少欧拉那种“x，y代入其他未知数”的变量分析法，婆罗摩笈多只能围绕自然余数1，设立一套构作整除式的法则。利用余数1从三个角度做文章，涉及它的值1，涉及商个数的奇、偶，还有产生余数1的相应除数，构作整除式。

为此，不得不设定严格的前提：如不定方程137x+10=60y附加数为正，紧跟在大系数“ax”之后，形成特定的不定方程表达式。预处理附加数为1，成137x+1=60y，这才可以清点余数1时的商个数，作出加减的判断：奇数时为加，偶数时为减。

于是有（术文2）：“对余数单位1乘以一个所选择的数，使得乘积减去1（或者加上1，当商个数为奇数时），将可以由产生余数单位1的相应除数所整除。”我们称整除式。分母，就是“产生余数单位1的相应除数”，也就是8。分子有两项，由乘积与加、减附加数所组成。

一是乘积：“余数单位1乘以一个所选择的数”，可从所选择的数，谋求整除。

另一项为加、减1，以适应整数对的奇序、偶序，规律是：当商个数为偶数时，减去1，作为主体，写在正文中；当商个数为奇数时，加上1，作为辅助，置于括号内。

注意，不定方程137x+1=60y，余数1的商个数4是偶数，137和60是偶序整数对。这是（术文2）正文的说法，不统计首商0。

取解式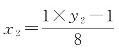以整除为目标，“我们选9作为选定数”，y2=9，整除得x2=1。

3　余数1商个数的奇偶变动

从阿耶波多不定方程137x+10=60y看，余数1的商个数是2，3，1，1中第4个，4为偶数。这是（术文2）中正文的说法，即不统计首商0，形成“乘积减去1”。

然而，（数例二2）的说法略有改动，承认60=137×0+60的首商0，余数1的商个数变成0，2，3，1，1中第5个，5为奇数。

因此，数例2的商个数为奇数，还是出现1×9-1，即术文中的“乘积减去1”。

相应地，（术文2）中辅助的括号“或者加上1，当商个数为奇数时”，指另外一类奇序整数对。60x+16=13y，两系数辗转相除到自然余数1而止：2y2=3x2+1。商个数为5，奇数，构造出整除式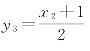，用的是“加上1”。参见18.4.3。

4　取解式和初解

两系数辗转相除，常数同时参与辗转相除，得到一系列降系数不定方程。利用某个降系数不定方程，取出整数解。

这个取出整数解的式子称为取解式。取解式的解称作初解（初步的解）。

需要回代入这一系列降系数方程，才得到原不定方程的通解和特解。

取解式各有不同，可以与余数0相关，也可以与余数1相关。

整除式取解，必取“所选择的数”y2=9，才出现x2=1。初解只能写成y2=9和x2=1。

可见，以整除式取解，只利用余数1，与余数0无关。

5　依赖性的应用

最后，婆罗摩笈多依赖137x+1=60y的解，去解出阿耶波多不定方程137x+10=60y。

以x=7，y=16乘10，得x=70，y=160。

再各除以对方系数，得x=70÷60余10，y=160÷137余23。所以x=10，y=23是137x=60y-10的一组最小正整数解。核算：137×10=1370=23×60-10。

可见x=10，y=23是不定方程137x+10=60y的一组特殊解。

18.4.2　偶序整数对数例

阿耶波多不定方程系数是偶序整数对数例。按照术文1，辗转相除时“依次记下商值”。再按（术文3）“在上列商值之下，放置这个所选定的数，此后再放置刚求得的商值”，放置初解y2=9和x2=1。

我们可以按印度人氏的习惯，把运算排成图式（图18.2）。

图18.2　137x+1=60y的习惯图式

最后按照（术文3）恒值粉碎机求法。“对于最后数，加上中间数与下一个前置项的乘积（等等）。所找到数，或其经约简除数的除法之后的余数，就是恒值粉碎机。”

实行回代，1是最后数，9是中间数，1是前置项。1+1×9=10，9+1×10=19，10+3×19=67，19+2×67=153。153是恒值粉碎机。代入60y=137x+1，即有60×153=137×67+1。

这个153，除以137，余数7，就是最后得到60y=137x+1的解x=7。我们现在称作最小正整数解。正如（数例二3）所说：“据说可如前一样找到恒值粉碎机。”婆罗摩笈多的60y=137x+1，附加数+1是恒值，x=7称为恒值粉碎机。

有了恒值粉碎机，求解附加数10倍的60y=137x+10十分方便。“它与10的乘积可被60除，以得到所需的乘数10；10×137+10=60×23。”把x=7，乘以附加数10，得乘积70。70除以60，得70=1×60+10，才是乘数10。于是得到60y=137x+10的一个解x=10。核算：137×10+10=1370+10=1380=60×23。

18.4.3　奇序整数对数例

再举一个奇序整数对数例。借用婆什迦罗《莉拉沃蒂》第251诗节数据，求解附加数16的60x+16=13y。这里，60和13是奇序整数对。

我们先通过欧拉“x，y代入其他未知数”的变量分析法，得知附加数1的60x+1=13y的初解，x2=1时，有y3=1。再解出不定方程60x+16=13y。见表18.5。

表18.5　60x+16=13y的变量分析表

婆罗摩笈多没有变量代换，只能用辗转相除法的用语，刻画整除式。据术文2，“对余数单位1乘以一个所选择的数，使得乘积减去1（或者加上1，当商个数为奇数时），将可以由产生余数单位1的相应除数所整除”。自然余数1的除法是3=2×1+1，余数1乘以“所选择的数”x2，乘积1×x2“加上1”，除以除数2，取解式为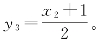

于是，取解式为，当x2=1时，有y3=1，这是初值。回代，x=8，y=37是不定方程60x+1=13y的一组特解。核算：60×8+1=480+1=481=13×37。

以x=8，y=37乘以16：x=8×16=128，y=37×16=592。除以对方系数后，得128=13×9+11，592=60×9+52。故不定方程60x+16=13y一组特解是x=11，y=52。核算：60×11+16=480+16=676=13×52。

可见，恒值粉碎机解法，能处理一切二元一次不定方程。

18.5　库达卡探源

就所见印度数学史早期史料看，库达卡极为简陋，隐晦难晓。

库达卡原意为碾细，“把问题击打成粉末”，涉及二元一次不定方程求解。公认，把a，b用辗转相除法互除，使余数越除越小，从而可设法求解。

但印度数学史中，又把库达卡解释为“乘数”[8]，记为x。

可见这类库达卡的描述，似乎浮于泛泛而谈。

数学史研究，只能根据史料事实说话。1999年王渝生[9]指出的：“算理上的分析并不能代替对历史事实的确定，任何结论都必须有史料上的依据”，无论对中国数学史还是印度数学史，都是至理名言。

公元6世纪婆罗摩笈多的恒值粉碎机解法，严格确定二元一次方程表达规则，两次重复辗转相除，巧妙地保证余数为1。利用求得1的除法，设定法则，构造整除式。选定“选择的数”，利用整除，求出相对于附加数1不定方程的解，称作恒值粉碎机。再借以求出附加数非1的不定方程。

可见，婆罗摩笈多解法恒值粉碎机的原术、原意，是依附于余数1的整除式，不能用于依附于余数0的降系数不定方程解法。

我们还找到一条恒值粉碎机资料。印度学者早已熟知余数1与附加数1的关联作用。

860年Pᶉthûdakasvâmî说，不定方程by=ax+1一般称为恒值粉碎机[10]117。恒值粉碎机源于分类机（±1）是不变的、永恒的。

关于早年印度不定分析的这个解释，离婆罗摩笈多（梵藏）年代最近，值得注意。

只有结合本书第6章“单一不定分析式”中关于解过渡和解转换的研究，深入挖掘婆罗摩笈多的恒值粉碎机解法，才能探索古印度库达卡的源流。

参考文献

[1]Gupta R C,Mesra P O,Datta B.Historian of Indian Mathematics[M].Historia Mathematica 7.New York:Elsevier Inc.,1980:126-133.

[2]Datta B.Elder Aryabhata's Rule for the Solution of Indeterminate Equations of the First Degree[J].Bulletin of the Calcutta Mathematical Society,1932,24:35-53.

[3]Datta S,Singh A N.History of Hindu MathematicsⅡ[M].Delhi(India):Bharatiya Kala Prakashan,2001:98-110,reprint.

[4]沈康身.库达卡与大衍求一术[C]//吴文俊.秦九韶与数书九章.北京：北京师范大学出版社，1987：253-268.

[5]同[3].

[6]同[4].

[7]婆什迦罗.莉拉沃蒂[M].林隆夫，译注.徐泽林，等译.北京：科学出版社，2008：175.

[8]同[7].

[9]王渝生.算学志[M].中国算学史.上海：上海人民出版社，2006：291.

[10]同[3].