16.2.3 数学突破
遥远星空上周而复始的天体运动，历法编撰的需求，刺激出各种数学分支的萌芽。
中国古代历法灿烂辉煌，历法数学是世界数学史上的奇葩。
1932年，钱宝琮[5]指出：“古代算学本为天文历法之附庸。”
天文历法本来深奥难解，文明之初的探索神秘莫测，书录时回避要害，又不免闪烁其词，现存史料更易残缺不全。要想只凭若干数值挖掘内在关联，揣摩古代算法，谈何容易。
我国历法之完备而见于史册者，以三统历为最古。三统历假托黄钟，附会易著，玄妙其词，后人读之，视为高深，莫可究诘。
清代乾嘉学派的钱大昕、李锐、董祐诚、陈澧、成蓉镜等学者，或重在正伪舛、脱误、去衍，或重在详细解释基本数据，或重在以本法推算、算术缀之，多方位研究汉武帝时代的三统历。李锐对中国历法史研究的贡献是不可磨灭的。李锐在《日法朔余强弱考》中第一个涉及了求一问题，并用来解二元一次不定方程。
近代三统历研究上最重大的两个数学突破是吕子方[6]做出的。一个是大周三算法，一个是数学上的连分数算法，我们称密近简化算法。
张秀熟为吕子方的《中国科学技术史论文集》作序，称：“著名物理学家、四川大学教授吕子方先生殁后十又八年，生平所著关于中国古代科技史的论文，始得由中国科学院成都分院自然辩证法研究室搜集、整理、校订，四川人民出版社编辑出版，与当代广大学者见面，作进一步共同探讨，此诚我国学术界一件盛事。”
中共四川省委原书记杨超曾为此书题词：“发展科学，振兴中华。”
1951年5月，吕子方“以科学实测为基础，以探讨三统历法，故第一章统母、第二章纪母，纯以实测及古传数字为出发点，以求所用基本数字之来源。如日法八十一，木星大周年数为一千七百二十八等是也。”何鲁为之作序，盛赞吕子方的突破：“析以新法，动中窾要，尤能明古人之用心，使二千年前之成绩焕然一新，厥功甚伟。”
吕子方所说日法81、木星大周1728，是密近简化分数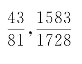
分母，适应历法编排的需要。
此说引起学术界热议，但吕子方直接用现代术语连分数描述2000年前的数值操作，充其量涉及存在性，未曾涉及构造性，不免难以迅速获得公认。
1999年，王渝生[7]对历法数学中的研究，纵论针砭，深中肯綮：
历法中的绝大多数数据都应该是科学地选取和经过运算，符合实际天文观察，因而是有一定方法的。所谓“调日法”就是如此。唐一行、北宋周琮、南宋秦九韶、清李锐都对其有不同的解释，我们也只能提出一点管见。况且，算理上的分析并不能代替对历史事实的确定，任何结论都必须有史料上的依据。“例不十，法不立”，仅有孤证那是不够的。
岁月悠悠，战乱频仍，典著茫茫，更有豕亥鱼鲁难免，相关直接史料的寻找，几无可能。
近百年来，围绕连分数的历法应用的论争，告诫我们仔细掂量掂量手中依仗的算理分析。
研究古人数值解法，我们无意求助于现代符号公式的展现，而是既考核现代数学原理，更关注传统数学筹算原图。我们所命名的密近简化算法，毕竟只是一厢情愿之词。
不能不感叹，刘歆刻意凑合计算岁星岁数的基础数据，再挂靠周易“乾坤之策”，这种荒诞之举竟成了不可或缺的过硬史料。前有岁星纪年法12岁作小周，后有岁星超辰的延伸，刘歆应用密近简化算法研究木星大周，来龙去脉，一清二楚。