16.2.4　人造行星数例

1962年华罗庚以人造行星、地球绕太阳运行为例，深入浅出地介绍怎样估算人造行星发射后再次接近地球的时间[8]。为与天度圈有别，我们用括号加注基准圈，简述如下。

假定地球绕太阳一圈（基准圈1年，太阳视运动为1年）360天（基准圈的划分），人造行星绕太阳一圈450天。因450和360的最小公倍数是1800或450 360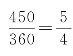，5年后，人造行星走4圈，再次接近地球。

地球绕太阳一圈，重新划分成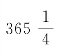天（基准圈的划分）。人造行星仍然是绕一圈450天。

顺便说说，因为基准圈的划分不同，所说的两个450天，时长不等。

我们意识到，渐近分数接近程度越高，分子、分母数值越大。反过来，降低分子、分母数值的位数，就有可能取得简化的渐近分数。

华罗庚的人造行星数例，帮助我们认识天度圈、日行一度、历数的实践意义和理论意义。正是天度圈圈数之比蕴含的巨大潜力，刺激出密近简化算法，更进一步刺激出大衍术求解满去式，算出上元积年。