4.1 早期的百鸡问题
《九章算术》成书于公元1世纪左右,其作者已不可考。西汉张苍、耿寿昌增补和整理时,《九章算术》已大体成形。再经历代各家增补修订,才逐渐成为现今定本。最后成书最迟在东汉前期。现今流传的大多是在三国时期魏元帝景元四年(263年),刘徽为《九章算术》所作的注本。
《九章算术》提出的不定方程如下:
今有五家共井,甲二绠不足,如乙一绠;乙三绠不足,如丙一绠;丙四绠不足,如丁一绠;丁五绠不足,如戊一绠;戊六绠不足,如甲一绠。如各得所不足一绠,皆逮。问井深、绠长各几何?
意思是说:五家人共用一井,甲用绳量井深,绳子的二倍尚不够,所缺恰好等于乙绳长。乙用绳子的三倍尚不够,所缺恰与丙之绳长一致。依次类推。问井深、绳子各多少?
这就是《九章算术》“方程”章的五家共井问题,按现今代数方法,可列出类似方程组:
2x+y=w,3y+z=w,4z+u=w,5u+v=w,6v+x=w。
其中x,y,z,u,v代表五家绠长,w代表井深。用消元法求得各家绠长与井深之比:
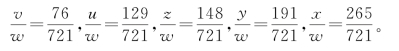
《九章算术》依方程术演算,并给出一组答案。刘徽注指出,此乃“举率以言之”,意指问题的解答是无穷多组彼此成比例的数,这仅是其中互素的一组整数解。
遗憾的是,这种特殊的一次齐次问题可按方程术求解,却不能引导出新的方法与理论。严格地说,五家共井问题并不属于不定分析的范围,因为不一定要求整数解。但其解题方法,对后人是有影响的。
百鸡问题最早见于大约公元5世纪末成书的《张邱建算经》。
今有鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一。凡百钱,买鸡百只。问鸡翁、母、雏各几何?
显然,如果设公、母、小鸡各为x,y,z只,那么这是一道三个未知数、两个方程的不定问题。在x,y,z都必须是自然数的约束下,实际上只有有限组解。
全部三组自然数解分别是:其一,公鸡4只20钱、母鸡18只54钱、小鸡78只26钱;其二,公鸡8只40钱、母鸡11只33钱、小鸡81只27钱;其三,公鸡12只60钱、母鸡4只12钱、小鸡84只28钱。
《张丘建算经》的“术”,表明了各组解之间的关系:
鸡翁每增四、鸡母每减七、鸡雏每益三,即得。
这就是说,公鸡每增加4个(增加20钱),母鸡就要减去7个(减少21钱),小鸡就要增加3个(增加1钱)。这一增减关系也是正确的,但是仅凭此无法得到全部解。
因此,我们可以说《张丘建算经》给出了正确解答及其之间的增减关系,但却没有给出求特解和增减关系的方法。
后世的探讨,沿着改进算题、求特解和求增减关系三条路线进行。(https://www.daowen.com)
徐岳(?—220),字公河,东莱(今莱州市)人,东汉数学家、天文学家,第一位“珠算”的提出者和“算盘”的记录者。东汉灵帝时,著名天文学家刘洪“按数术成算”创造了“乾象历”,并“亲授其法”予徐岳。
徐岳编撰《数术记遗》,卷首题“汉徐岳撰,北周汉中郡守、前司隶,臣甄鸾注”。成书年代不详。载有百鸡类问题两问。
其一:
今有鸡翁一只直五文;鸡母一只直四文;鸡儿一文得四只。今有钱一百文,买鸡大小一百只。问各几何?
其二:
今有鸡翁一只直四文;鸡母一只直三文;鸡儿三只值一文。今有钱一百文,还买鸡一百只。问各几何?
北周甄鸾(535—566)注《数术记遗》,称:“计数既捨数术,宜从心计”,并举百鸡题为计数之事。清代丁取忠在《数学拾遗》(1851年)中说,甄鸾定其术为“置钱一百在地,以九为法,除之得鸡母之数,不尽者反减下法为鸡翁之数”。甄鸾“去古未远,莫溯心源”,所说牵强附会,答数仅为偶合。
最早给出《张丘建算经》百鸡问题求特解方法的是唐宋之际的学者谢察微。
谢察微说,考虑到小鸡1钱3只,那么把100÷9得到11余1,11就是母鸡数。第二步用9减去余数1,得到8为公鸡数。第三步100-11-8=81为小鸡数。最后依据增减率得到其他解答。把这种解法合理化,可以说成是先取100钱的三分之一33钱为母鸡价,除以3得到母鸡数。不过第二、第三步无论如何是说不过去的,是不切实际的算法浪漫主义。
南宋杨辉《续古摘奇算法》引《辨古通源》(已失传)百鸡类题一问:
钱一百买温柑、绿橘、扁橘共一百枚。只云,温柑一枚七文、绿橘一枚三文、扁橘三枚一文。问各买几何?
另一题说:
醇酒7贯1斗、行酒3贯1斗、醨酒1贯3斗,十贯买酒十斗。
因为是三个未知数连动求解,杨辉认为此类问题是“三率分身”,后世称为“三色差分”。
上列四问,除《张邱建算经》给出三组正整数解外,其余均只写出一组答案。关于解法,《张邱建算经》术文仅十七个字:“鸡翁每增四,鸡母每减七,鸡雏每益三。即得。”
后人很难得其要旨,故在宋元丰七年秘书省刻书时,为《张邱建算经》添入谢察微术草之前的引言中,有“疑其从来脱漏阙文”字样。
南宋杨辉沿用并改进了这种方法,先用试算的方法确定一个未知数,然后求得另两个未知数。其后吴敬、程大位等人的解法都是沿用杨辉的思路。
明嘉靖三年(1524年),布衣数学家王文素完成《算学宝鉴》,对百鸡术有较大的推进。他的解法相当于先消去一个未知数,化为二元一次不定方程,然后通过试算求得一组解。王文素进而通过鸡值损益,给出增减关系的正确算法。除此之外,王文素不满足“三率分身”,探讨了最高达七个未知数两个方程的“众率分身”的问题。虽然其算法仍然具有试算的性质,但对百鸡问题的研究已经远超古人。为此,他得意地说:“愚乃玩之既久,得此拙法。虽十率以上亦可求之,岂止三率乎!”
《张邱建算经》以后,许多学者试图重解百鸡问题,但在骆腾凤以前的一千多年,竟无人获得成功。
