14.12.2 格的设立
秦九韶把求定现象归纳成格。苦于归纳标准不严，无法做到不重不漏，不得不设立一些另类现象，以示补充。
元数格第一，统领全局。
元数者，先以两两连环求等，约奇弗约偶[或约得五，而彼有十，乃约偶而弗约奇]。或元数俱偶，约毕可存一位见偶。或皆约而犹有类数存，姑置之，俟与其他约徧，而后乃与姑置者求等约之。或诸数皆不可尽类，则以诸元数命曰复数，以复数格入之。
元数格从两两连环求等入手。复数格则从“求总等，存一位，约众位”入手。
元数格中有两种情况：①约奇弗约偶；②元数俱偶，约毕可存一位见偶。
①中的注文“或约得五，而彼有十，乃约偶而弗约奇”，五是奇，十是偶。“约偶”指约十，还暗示了定数组不唯一。
馆臣在分粜推原题下有按语说：“五为中数，或约偶或约奇，皆可。”此题的问数组是83，110和135。按馆臣的奇偶观点，“或约偶”导致83，22，135，“或约奇”导致83，110，27，这两组都是定数组。
至于“元数俱偶”，如程行计地题100与4。等数4是偶数，无论除哪一个，都得一奇一偶。“约毕可存一位见偶”，约成数中有一个偶数。
“或皆约而犹有类数存，姑置之，俟与其他约徧，而后乃与姑置者求等约之”一句，秦九韶以“俟与其他约徧”，即两两连环求等，作为分界线。
我们曾说过，从操作手段来说，任何一组问数，两两之间求等相约，如某两数约后仍有等，“姑置之”，即这两数只约一次，不约第二次，直到两两连环毕。就数学实质而言，各约成数一定是相应问数的因数，各约成数的乘积一定是原来问数的最小公倍数，但各约成数之间并不一定两两互素。因此，只能称作准定数。
当各约成数乘积等于最小公倍数时，作为下一步的待约数，只要再求出等数，就是续等。凡续等，必须约一数复乘另一数，既保证两数互素，又保证最小公倍数不变。
因此，以“俟与其他约徧”作为判定续等的标准，恰巧与以最小公倍数作标准等价。此时这个等，肯定是续等，必须用来复乘。
秦九韶注意到这情况，但不明写复乘，却转向专门对付复乘的复数格，所以有第四段，用复数格处理。
一句话，秦九韶头脑中，衍母、（若干周期的）一会积和续等三个概念还是孤立的。
收数格第二。
收数者，乃命尾位分厘作单零，以进所问之数。定位讫，用元数格入之。或如意立数为母，收进分厘，以从所问，用通数格入之。
收数，取名于“收进分厘”。只有一题，古历会积题三百六十五日四分日之一“假令”成“三百六十五日二十五刻”，成了“尾位见分厘者”，也就作为收数的典型。但此题求定数具体计算中，没有当元数用过，说不上“定位讫，用元数格入之”，只是一条转化措施。
不考虑十进制因素的“收进分厘”，代之以“如意立数为母”，说成入通数格。
这么说来，收数格处理只是想当然，没有具体数例作背景，更没有理论上的推证。
通数格第三。
通数者，置问数通分内子，互乘之，皆曰通数。求总等，不约一位，约众位，得各元法数，用元数格入之。或诸母数繁，就分从省通之者，皆不用元各母，仍求总等，存一位，约众位，亦各得元法数，亦用元数格入之。
通数格根据特色操作，分成三段。特色操作是通分内子，只有一题古历会积题，冬至
，朔策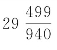
。特色操作用总等处理，即求总等，不约一位，约众位后，得各元法数。特色操作用“诸母数繁，就分从省通之，皆不用元各母”，还是“求总等，存一位，约众位，亦各得元法数”。
然而，推计土功题并没有与通数相关的数字例子。术文却在“得各县日筑复数”之后加注：“有分者通之，互乘之，得通数”。
复数格第四。
号称元数、收数、通数三格普遍适用的复乘求定之理，竟然只是从“急足之类”，即程行两题中硬凑出来的，详见本书14.12.6“复数格的原型”。