14.12.4 奇偶的应用
大多数学者公认：根据对《数书九章》所有数例的分析，多数情况下，奇是单数，偶是双数；当两数求等相约时，作为公约数单数倍的待约数叫奇，作为公约数双数倍的待约数叫偶。
例如，6和4有最大公约数2，6=2×3，4=2×2。3是单数，6称奇，因为6约得奇。
再举一例，100和4有公约数4，100=4×25，4=4×1。25是单数，所以100为奇。而100和4两者都为奇，因为约得的都为奇。
“两两连环求等”指一定的顺序求出每一对元数的最大公约数。“约奇弗约偶”指在一般情况下，用最大公约数去处理待约数，能使商为单数的那一个待约数被约出单数，而保持另一个不变，为双数，因为一单一双，达到互素的可能性最大。
例如，对待约数6和
意味着“约奇”，约成数3和4互素。因为3是单数，相应待约数6称作奇，化约后约成数只是有较大的互素可能性而已。
如果
意味着“约偶”，约成数6和2有公因数2，称为“两位见偶”。
再有，对待约数4和100，如果用4去约，一种可能是1和100，另一种可能是4和25。1和25都算得上单数，两种情况都叫“约奇”。但是，前者
导致“见一”，不得不设立补充原则“勿使见一太多”加以避免。于是，只能用后者
事实上，约奇的方法不能保证两个约成数互素，充其量只是一种较大可能性而已。
例如
，认定5是奇数，25是奇数。如果用“约奇”，所得[20，5]并不互素。改为“约偶弗约奇”，即5是奇数，约偶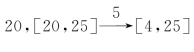
，才使得4和25互素。
显然，秦九韶意识到，“奇”“偶”功能有限，仅仅是探索使约成数互素的拐杖而已。
在积尺寻源题中，他企图避开“奇”和“偶”，寻求一个新方向，把数和位紧紧结合起来。把问数从小到大排列，“假八音为号位”，用当时流行的音调给位起名，便于区别。“先以小者”作主位，同其他数位求等相约，尽可能约大的数位。若这样做无法使约后互素，则“反约”自身。在这个冗长的求定算草中，只字不提“奇”“偶”字样。
但是，他仍然没法彻底解决最大公约数和补偿素因数最高次幂之间的关系，仅因此题数据特殊而没有暴露出问题来。
从理论完美的角度看，使用素数与素因子分解的概念，可使方法的叙述比较漂亮、简捷，但从算法角度来看却不然。首先，化约模数时，素数与素因子分解的概念并不是必需的。进一步，即使引入这些概念，具体将一个数分解成素因子的积时，还需要一套可行的算法，这种算法的复杂程度，至少不亚于判断一数是否为素数的算法。而秦九韶化约模数的算法，主要是辗转相除法。因此，从算法上看，秦九韶的方法更简便易行[17]。