11.8.3 连分数简史
奥尔德斯认为，连分数思想最早期的线索是不甚明了的，因为许多古代的数学结果只是对这种分数的一种启发，当时并不存在这一课题的系统发展。
因此，奥尔德斯关于“连分数”起源的提法有这样三条。
求两个数最大公约数的欧几里得辗转相除法，在本质上就是把一个分数化为连分数的方法。这或许是连分数发展的最早的（公元前300年）重要一步。
第二条涉及印度数学家阿耶波多一世前文出现过的著作，出现过最早用连分数求线性不定方程一般解的尝试。
第三条，连分数一般概念的进一步线索，是偶然地在阿拉伯和希腊的著作中发现的。我们则认定连分数只是整数对现象一个分支，特征是渐近分数。
数学史研究只能根据史料事实说话。1999年王渝生指出的“算理上的分析并不能代替对历史事实的确定，任何结论都必须有史料上的依据”，确实是至理名言。
因此，我们以公元前104年密近简化算法作为连分数的萌芽。
西方人以连分数逐次删除尾部，形成渐近分数系列。其实，只要算出同一个商的两个序列值，就组成与两原整数之比近似的分数了。
早在公元前104年，落下闳把古六历的
密近简化计算为
，求出太初历的日法81。
中国人的密近简化算法是上元积年计算法的基础。如果没有发现以岁星岁数为代表的大周概念，我们真不知道怎样跨越1208年开禧历之前1200多年的漫长时光，去证明公元之初历法家已经知晓密近简化算法。
公元前7年，刘歆利用岁星纪年法12岁作小周，刻意凑合岁星岁数的基础数据，应用密近简化算法研究木星大周，挂靠周易“乾坤之策”，独创岁星超辰。
公元5世纪的祖冲之发扬密近简化算法，大胆提出了391年144闰的闰周新数据。祖冲之可能利用刘徽割圆术的“差幂”，实行补缀衔接，应用密近简化法，简捷明快求出胬数、盈数。再用密近简化法，求出圆周率的约率和密率。
早期西方数学家只是孤立地研究连分数的表达形式，逼近已知根号、已知分数等。
大多数权威认为，连分数的近代理论开始于蓬贝利。
这位意大利数学家生于波伦亚。1551年开始从事水利设计工作，参与基亚纳河谷沼泽地的开垦。1556年到1560年，他利用开垦间断时间撰写了《代数学》，在1572年出版了前3卷。后2卷手稿是1923年才被发现，1929年出版。该书从基本定义和符号入手，系统地总结了16世纪的代数方程理论，讨论了多种二、三、四次方程的求解，特别是解决了三次方程不可约的情况，并为此建立了虚数的运算法则。他还采用了若干较先进的代数符号，首次用连分数逼近平方根的值。例如，用现代符号来写
他的工作受到斯蒂文（Stevin，Simon，1548—1620）、莱布尼茨（Leibniz，Gottfried Wilhelm，1646—1716）等后继数学家的高度赞誉，影响很大。
西方第二个考虑连分数的是卡塔尔迪（Gataldi，Pietrn Antonio，1552—1626），也是波伦亚人。在一篇关于根理论的论文中，为了印刷方便，写成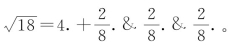
第三个西方作者是施温特（Schwenter，Damiel，1585—1636），法国阿尔特道夫大学教授，在不同的时间教过希伯来语、东方语和数学。在《实用几何》（Geometrica Practica）中求177和233的最大公约数，发现了求
的近似值的方法。通过计算，他定出了渐近分数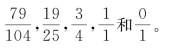
另一个使用连分数的卓越数学家是布龙克尔（Brouncker，William，1620—1684），他是皇家协会的第一任会长。他把英国数学家瓦里斯（Wallis，John，1616—1703）所发现的有趣的无穷乘积
转化为连分数
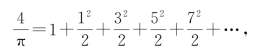
但是他没有给出这些分数的进一步应用。
在瓦里斯发表于1655年的《无穷小算术》（Arithmetica Infinitorum）一书中，讨论了布龙克尔的连分数，叙述了一般连分数的渐近分数的许多初等性质，其中包括它们的构成法则。他第一次使用了“连分数”这一术语。
伟大的荷兰数学家、力学家、天文学家和物理学家惠更斯（Huygens，Christiaan，1629—1695），为了给出天文馆齿轮的正确设计的一个好的近似，使用了连分数，并把此写进了论文《自动描述天象仪》（Descriptio Automati Planetarii）中，这篇论文在他去世后于1698年发表。
由此开始，像欧拉（Euler，1707—1783）、兰伯特（Lambert，1728—1777）、拉格朗日（Lagrange，1736—1813）等大数学家，以及其他数学家发展了我们今天所知道的理论。欧拉的重要论文《连分数》（1737年）为连分数的现代理论奠定了基础。