9.3 形式分数的分母值取1
当前中学教材中采用未知数代换的不定方程整数解法，公认源于1770年欧拉的通俗教本《代数》。我们称之为1770年欧拉的“形式分数的分母值取1”方案。
欧拉把原不定方程常数，同步参与两系数的辗转相除，引入新变量，出现形式上的分数，实质上的整数。整理新变量，可以得降系数不定方程。等到出现自然余数1，形式分数就因分母取1而体现整数值，从而体现了整数解。
鉴于狄克逊《数论史》的表述夹叙夹议，我们直接引用文献“Algebra，2，1770，§4-23；French Transl.，Lyon，2，1774：5-29；Opera Omnia，（1），I：326-339”（原书所列文献，原格式抄录），但数例记作5x=7y+3。
为全书统一，我们采用“大系数项ax”约定，先行交换未知数字母，成为5y=7x+3。后继字母，采用带脚注的x1，y1等替换文中的z，u等。这种做法不会影响理解欧拉原意，将来可适用于印度库达卡的研究。
欧拉用了总是以较小数为除数的方法，本质上是紧随着罗尔。对于5y=7x+3，有
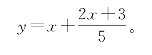
分子必然是5的倍数，这样有2x+3=5y1，
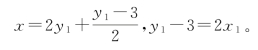
因而，x=5x1+6，y=7x1+9。他表明，这个过程等价于求5和7最大公约数的过程：
7=1×5+2, x=1×y+y1,
5=2×2+1, y=2×y1+x1,
2=2×1+0, y1=2×x1+3。
这个过程等价于求5和7最大公约数的过程，求出自然余数1和余数0（表9.1）。这里着重分析引入新变量的作用。
表9.1 5y=7x+3的变量分析
“分子（2x+3）必然是5的倍数”一语，描述的是形式分数，所说倍数值是y1，整数。引入新变量y1（z）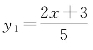
，整理得2x+3=5y1。
第二次除法5=2×2+1，得自然余数1，
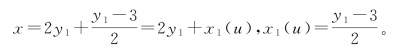
最后余数0除法的除数1，成为形式分数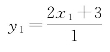
的分母，形式分数消失，为整数2x1+3。
变量分析表中，回代用双等号区分。
以最后引入变量x1作任意整数，得到x=5x1+6，y=7x1+9，就是5y=7x+3的一般解。