17.4.1 刘徽不等式由来
秦汉以前,人们以“径一周三”为圆周率,称古率。
后来发现,圆周率应是“圆径一而周三有余”。入汉以后,圆周率的计算吸引了许多科学家的注意,如刘歆、张衡、刘徽、王蕃、皮延宗等人都做了不少工作。
公元前1世纪成书的《九章算术》,提出圆田术:
术曰:半周半径相乘得积步。
设周长l,半径r,面积S,则
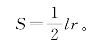
又术曰:周径相乘,四而一。即
![]()
为证明圆田术,公元263年的刘徽创造了割圆术(图17.1)。
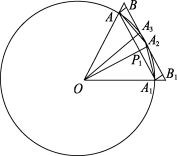
图17.1 割圆术示意图
从圆内接正六边形开始,边数不断加倍,多边形面积与圆面积的差就越来越小。正多边形的边数不能再加的时候,其面积的极限就是圆面积。余径是边心距和圆径之差。正多边形的边长乘以余径,形成小矩形。
同一次分割下,若干小矩形的集合组成“类齿轮盘”[11],骑跨在圆周上。
一次次分割衍生出一层层类齿轮盘,都可分拆成余径为高的等腰三角形,面积为差幂,以及两小勾股形之和,面积等同差幂。
到极限状态,正多边形与圆相合,余径消失,类齿轮盘面积就不至于突出在圆周之外了。
以六觚之一面乘一弧半径,三之,得十二觚之幂。若又割之,次以十二觚之一面乘一弧之半径,六之,则得二十四觚之幂。割之弥细,所失弥少,割之又割,以至不可割,则与圆周合体,而无所失矣。觚面之外,犹有余径,以面乘余径,则幂出弧表。若夫觚之细者,与圆合体,则表无余径。表无余径,则幂不外出矣。以一面乘半径,觚而裁之,每辄自倍。故以半周乘半径而为圆幂。此以周、径,谓至然之数,非周三径一之率也。
“割六觚以为十二觚术”展示如下:
取直径2尺的圆,内接正六边形S6的边长为1尺。设一边AA1,过圆心O作AA1的垂线OA2,交AA1于P1,交圆周于A2,则AA2就是内接正12边形的一边。勾股形AOP1中,OA=1尺为弦,
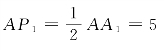
![]() (https://www.daowen.com)
(https://www.daowen.com)
![]()
![]()
![]()
注意,图17.1“割圆术示意图”中,处于在正6边形一边与圆之间的余径为P1A2。过A2点作OA2的垂线,处于圆外。过A点作线段AB垂直于AA1,交该垂线于B。过A1点作线段A1B1垂直于AA1,交该垂线于B1,构成小矩形AA1B1B。
以余径P1A2为高的等腰三角形AA1A2,共6个,面积是“差幂”(S12-S6)。以余径乘正多边形的边长AA1为小矩形AA1B1B的边长,共6个。六只的面积为两倍的“差幂”:2(S12-S6),是骑跨在圆周上的“类齿轮盘”。
然后,陆续展示“割十二觚以为二十四觚术”、“割二十四觚以为四十八觚术”和“割四十八觚以为九十六觚术”。即从正六边形开始,依次将边数加倍,求出正12,24,48,96等正多边形的边长,从而算得正24,48,96,192等边形的面积。涉及数据见下表(表17.8),斜线表示未曾计算。
表17.8 刘徽割圆数据
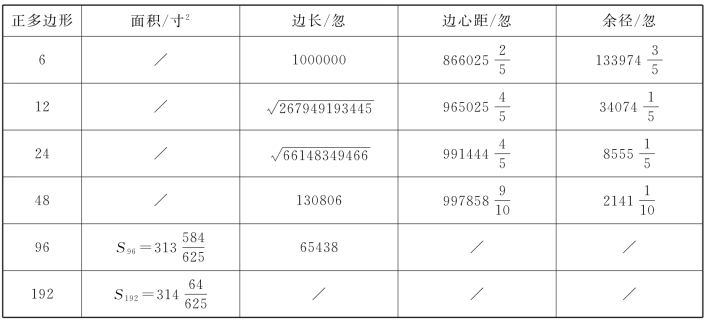
下面讲割九十六觚以为一百九十二觚术,原文如下:
以半径一尺乘之,又以四十八乘之,得幂三万一千四百一十亿二千四百万忽,以百亿除之,得幂三百一十四寸六百二十五分寸之六十四,即一百九十二觚之幂也。以九十六觚之幂减之,余六百二十五分寸之一百五,谓之差幂。倍之,为分寸之二百一十,即九十六觚之外弧田九十六所,谓以弦乘知之凡幂也。加此幂于九十六觚之幂,得三百一十四寸六百二十五分寸之一百六十九,则出于圆之表矣。故还就一百九十二觚之全幂三百一十四寸以为圆幂之定率,而弃其余分。以半径一尺除圆幂,倍所得,六尺二寸八分,即周数。……又令径二尺与周六尺二寸八分相约,周得一百五十七,径得五十,则其相与之率也。周率犹为微少也。
求出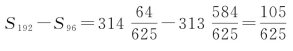 ,是为差幂:“一百九十二觚之幂也,以九十六觚之幂减之,余六百二十五分寸之一百五,谓之差幂。倍之,为分寸之二百一十,即九十六觚之外弧田九十六所,谓以弦乘知之凡幂也”,说的是“类齿轮盘”。这正96多边形的96条边,乘余径,构成96只小矩形,总面积为
,是为差幂:“一百九十二觚之幂也,以九十六觚之幂减之,余六百二十五分寸之一百五,谓之差幂。倍之,为分寸之二百一十,即九十六觚之外弧田九十六所,谓以弦乘知之凡幂也”,说的是“类齿轮盘”。这正96多边形的96条边,乘余径,构成96只小矩形,总面积为![]() 。“加此幂于九十六觚之幂,得三百一十四寸六百二十五分寸之一百六十九,则出于圆之表矣。”
。“加此幂于九十六觚之幂,得三百一十四寸六百二十五分寸之一百六十九,则出于圆之表矣。”
于是,
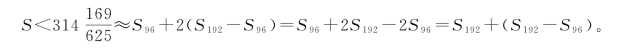
左边直观地添上圆内接正192多边形的面积S192,就是
![]()
这样,分析差幂,我们得到刘徽不等式,再列出一般式:
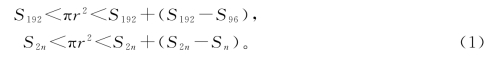
算到圆内接正96边形的面积S96,可求得圆周率![]() ,相当于π=3.14。
,相当于π=3.14。
而觚差幂六百二十五分寸之一百五。以一百九十二觚之幂以率消息,当取此分寸之三十六,以增于一百九十二觚之幂,以为圆幂,三百一十四寸二十五分寸之四。……以半径一尺除圆幂三百一十四寸二十五分寸之四,倍所得,六尺二十八分二十五分分之八,即周数也。全径二尺与周数通相约,径得一千二百五十,周得三千九百二十七,即其相与之率。若比者,盖尽其纤微矣。举而用之,上法为约耳。当求一千五百三十六觚之一面,得三千七十二觚之幂,而裁其微分,数亦宜然,重其验耳。
刘徽还进一步算到圆内接正3072边形的面积S3072,推算了圆周率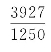 ,相当于π=3.1416。
,相当于π=3.1416。
