17.1.2 闰周的计算
我们回顾一下闰周的由来和发展。
公元前500年左右，人们就目测观天，最基础的数据就是太阳周天19次，月球周天235次，日月相会于星空背景原点。经过19年，每年12月，共12×19=228，235-228=7，这就是19年7闰，称之为闰周。
从春秋战国到秦朝时期制定的黄帝、颛顼、夏、殷、周、鲁六种历法，称为古六历。
古六历的岁实、朔策，都利用了近似的闰周19年7闰。
学者公认，古人把尽可能准确的天象观察和数学方法有机地结合起来，牺牲步朔的一点点精度，折中协调年、月、日长度，所推出误差约661秒的回归年长度
日，也可能为当时粗略的圭表测量所证实。使用近似的置闰规则19年7闰。因日的分母4，4×19=76年。这76年含
日，含朔望月940个，其中平常月12×76=912个，闰月7×4=28个。相除得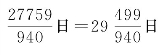
，称为朔策，误差约23秒。
由
可以发展出古代历法中一系列重要数据。
根据古六历
，落下闳用密近简化法，计算出太初历的
刘歆在940和499序列值计算表中，算到除法12=11×1+1（r7）（自然余数）。再算下一步，是11=1×10+1（r8）（调节余数）。筹算板上下，1（r8）=1（r7），合称等数。
刘歆的突出贡献是把两个余数1组成的等数1引入为标志，用来关联81与43。
关于密近简化法的计算，我们有两个注意点：
一是序列值计算容易失误。
余数为0时的序列值等于入算数。利用这一点，可以保证序列值计算表一步成功。如果入算整数对有最大公约数，余数为0时的序列值就等于约简的入算数。参见11.3.5。
二是只凭密近简化计算表，无法察觉其数据的更改。
我们回顾一下，当初断定刘歆曾经做过人为改动，全凭三统历原文。纪母说：“木金相乘为十二，是为岁星小周。小周乘巛（坤字古体）策，为千七百二十八，是为岁星岁数。”我们从岁星12年11见，据三统历岁实，算出岁星会合周期值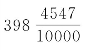
日。再根据1728岁认作岁星岁数，1583次认作见数，145认作岁星周天数。用密近简化法逆算出，刘歆采用
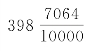日。没有这样的证据对比，是无法判断刘歆人为改动的。