18.2.1 降系数不定方程来源
达生、辛格按自然余数1商个数的奇偶，把整数对分成两大类。把两系数辗转相除到余数1、余数0，列为情况ⅰ。情况ⅱ，则指辗转相除中途结束，并未求到余数1、余数0。
降系数不定方程的字母体系与脚码繁复难记。为方便读者，我们以阿耶波多不定方程137x+10=60y为例，属于ax+c=by（I），附加数c紧随大系数ax。因137x+10=60y，两系数137和60辗转相除，自然余数r4=1的除法序数是4，为偶数。因此，137和60为偶序整数对。
依据欧拉变量代换基本思路，列出偶序整数对的降系数不定方程演算表（表18.1）。
表18.1 偶序整数对137与60降系数不定方程
第4次除法出现自然余数1（r4），引入新变量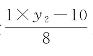
，整理成降系数不定方程8x2+10=y2。
第5次除法为余数0，没有引入新变量，整理成8x2=1×y2-10，也是降系数不定方程。
下面，我们逐字翻译英文版[5]（2001年最新版）第86到99页，达生、辛格的降系数不定方程的解法。对核心段落情况（ⅰ.1），即偶序整数对且辗转相除到余数0的这一段，特地插入方括号的编号注释。
偶序整数对137和60辗转相除，余数为0时，商总个数5，奇数。第4次除法9=8×1+1得余数1，商个数4，为偶数。脚注中，记n=2，于是，2n=4，2n-1=3。
这里展示的降系数不定方程解法，属于1770年欧拉的“形式分数的分母值取1”方案的思路，不列作单独的解法。参见本书11.2.1“解法分类”。
我们发现，达生、辛格处理不慎，瑕疵不少。
译文“情况（ⅰ.1）设商个数为偶数”一条，“方程（I.2n）和（I.2n+1）就分别变成yn=q2nxn+c，而yn+1=c”中，yn=q2nxn+c就是个瑕疵，应为yn=q2nxn-c，即降系数不定方程为8x2=1×y2-10，y3=10。
后面的“q2n=r2n-1”为q4=r3，我们代入q4=1，r3=8，得到1=8，又是个瑕疵。
后面的“情况（ⅰ.2）设商个数为奇数……q2n-1=r2n-2”，为同样的错误。
假如R1＞R2，所解的不定方程是ax+c=by（I），这里，a，b互素。
这样，我们有[原注：当a＜b时，有q=0，r1=a]
a=bq+r1,
b=r1q1+r2,
r1=r2q2+r3,
r2=r3q3+r4,
…
rm-2=rm-1qm-1+rm,
rm-1=rmqm+rm+1。
[注1：商q脚码从数字0起，如y=qx+y1。库文用q1，相差1，不影响计算。依次类推。]
现在在方程（I）中代入a的值，有by=（bq+r1）x+c。因此，y=qx+y1，其中by1=r1x+c。
换句话说，因为a=bq+r1，置入y=qx+y1，方程（I）降低成by1=r1x+c（I.1）。
[注2：相当于把（I）137x=60y+10演化成为降系数不定方程60y1=17x+10（I.1）。]
同样，因b=r1q1+r2，类似地置入x=q1y1+x1，方程（I.1）进一步降低成r1x1=r2y1-c，等等。
[注3：相当于把（I.1）60y1=17x+10演化成为降系数不定方程17x1=9y1-10（I.2）。]
分列写出一系列的值和降系数不定方程，我们有
(1)y=qx+y1, by1=r1x+c; (I.1)
(2)x=q1y1+x1, r1x1=r2y1-c; (I.2)
(3)y1=q2x1+y2, r2y2=r3x1+c; (I.3)
(4)x1=q3y2+x2, r3x2=r4y2-c; (I.4)
…, …;
(2n-1)yn-1=q2n-2xn-1+yn, r2n-2yn=r2n-1xn-1+c; (I.2n-1)
(2n) xn-1=q2n-1yn+xn, r2n-1xn=r2nyn-c; (I.2n)
(2n+1)yn=q2nxn+yn+1, r2nyn+1=r2n+1xn+c。 (I.2n+1)
[注4：降系数不定方程（I.4），r3x2=r4y2-c，常数c前是减号。这是正确的。]
于是辗转相除法能继续演算，或（ⅰ）到结束，或（ⅱ）得到一系列商，再终止。这两种情况下，所发现商的个数，忽略第一个（q），如同阿耶波多说，可以是奇的，可以是偶的。
[注5：相当于回代过程中，只求出不定方程的x值，省略求y值。不影响计算。]
情况（ⅰ） 首先假定辗转相除法能继续演算，直到余数零。因为a，b互素，倒数一个余数是单位1。
情况（ⅰ.1） 设商个数为偶数，我们有r2n=1，r2n+1=0，q2n=r2n-1。
[注6：辗转相除过程中，只有除数与被除数更替交换，事实上，不可能出现商q2n=余数r2n-1。]
方程（I.2n）和（I.2n+1）就分别变成yn=q2nxn+c，而yn+1=c。[注7：即方程（I.4）和（I.5）就分别变成y2=q4x2-10，而y3=10。误把常数前的减号变成加号，见注4。]赋予xn适当的整数值（t），我们得到yn的整值。[注8：赋予x2适当的整数值t，不妨说t=0。就得到y3=q=10，得到y3的整值。]就此，我们能从（2n）找到xn-1的值。一步步往回推算，最后求出x，y正整数值。从而解出方程（I）。
情况（ⅰ.2）设商个数奇数，我们有r2n-1=1，r2n=0，q2n-1=r2n-2。方程（2n+1）和（I.2n+1）可省略，方程（I.2n-1）和（I.2n）就分别降系数，变成xn-1=q2n-1yn-c，而xn=-c。
[注9：事实上，辗转相除过程中，不可能出现商q2n-1=余数r2n-2。]
赋予yn适当的整数值（t′），我们得到xn-1的整值。如前一步步往回推算，我们求出x，y整数值。
情况（ⅱ） 下面假定辗转相除法在得到一个奇的或偶的商个数之后，终止。
情况(ⅱ.1) 设商个数为偶数,原方程的降系数形式是r2nyn+1=r2n+1xn+c或
。如赋予xn以适当的整数值t,使得
是一个整数,据(2n+1)我们有yn的整值。如前,我们求出x,y的整数值。
情况(ⅱ.2)设商个数奇数,商[误。注10:原文就误作quotient]的降系数形式是r2n-1xn=q2nyn-c,或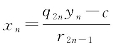
。如赋予yn=t′,t′是整数,使得
是一个整数。据(2n)我们找到xn-1的整值。故求出x,y整数值。
注意,情况(ⅰ)中求到余数0,肯定采用降系数不定方程,作为取解式。
情况(ⅱ)中,辗转相除不达到余数1、余数0,只是说商个数有偶数、有奇数,无法确定取解式。只说成是降系数不定方程r2nyn+1=r2n+1xn+c,或者是整除式
注意，情况（ⅰ）中求到余数0，肯定采用降系数不定方程，作为取解式。
情况（ⅱ）中，辗转相除不达到余数1、余数0，只是说商个数有偶数、有奇数，无法确定取解式。只说成是降系数不定方程r2nyn+1=r2n+1xn+c，或者是整除式
。
我们更发现，依现代辗转相除为背景的降系数不定方程以余数0为背景，与原始辗转相除为背景的整除式混为一谈，就会犯错。恰巧，库文就提供了这样的典型。