8.2 哥庭根抄本
与慕尼黑抄本差不多同时的另一抄本,称为哥庭根抄本,约成书于1550年。其中记载的一些不定分析问题,对于两两互素的模数,可以说给出了完全的解。对于非两两互素的模数来说,没有给出解的一般法则。
今将其中有关问题及解法,用现代符号摘译如下:
1 当模数两两互素时
N≡5(mod 7)≡7(mod 8)≡6(mod 9)≡0(mod 11)。
解 (1)8×9×11=792, (2)7×9×11=693,
792-n×7=1; 693-n×8=5;
(3)7×8×11=616, (4)7×8×9=504,
616-n×9=4; 504-n×11=9。
(1)式的余数是1,同余式已经解决了。(2)式的余数是5,它必须“约简”。其方法如下:
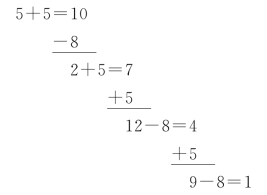
计算劳卡的量,为5个5。5是同余式的解。

由上式可知,(2)式合计5个5,(3)式合计7个4,(4)式合计5个9。这就是作者所说计算得(2)式的“劳卡(Loca)”是5,(3)式是7,(4)式是5。作者还就上式做了解释,他以(4)式为例说:“如果取504为‘约简的数’,则余数为9。如果取其(504)两倍,则余数9也得二倍起来。因之,除以11则余7。其他仿此。”
我们看到,高斯剩余定理中,伴随数的值“α是由式子1/BCD等(mod A)的一个值(最好是最小值),用BCD等所乘”。式子1/BCD等(mod A)相当于现今我们熟悉的同余式:
(BCD等)x≡1(mod A)。
这就是说,高斯定理中,是一揽子解出的,哥庭根抄本则分两步走:第一步,求其他模之积除以本模的余数。第二步,把余数相加若干次,这个次数,称为劳卡。
作者进一步说:“每一数除以自己的除数则余数为1,此外,可整除以其他除数。在‘约简的数’中,乘以其余数后,其余数仍然是其原来的余数。因此,每个‘约简的数’除以自己的除数则有一余数,而可整除以其他除数。所以,其和54087除以各除数时,则各有余数。”作者的这段论述用现代符号表示如下:(https://www.daowen.com)

其中,n=9。
2 当模数非两两互素时
N≡2(mod 6)≡6(mod 8)≡4(mod 10)≡8(mod 14)。
解法如下: L.C.M.(6,8,10,14)=840最小公倍数
840÷6=140 140≡2(mod 6)
840÷8=105 105≡1(mod 8) →扩大630≡6(mod 8)
840÷10=84 84≡4(mod 10)
840÷14=60 60≡4(mod 14) →扩大120≡8(mod 14)
140+630+84+120=974, 974-840=134。
但这并不是一般普遍适用的方法。正确解法的理由可发现自下列图示:

在最后的问题里,作者举例给出问题不可解的理由:
N≡4(mod 5)≡3(mod 6)≡2(mod 8)≡1(mod 9)。
这个问题模数的最小公倍数是360,而其“衍数”分别是72,60,45,40,因为6可整除60,所以a×6≡1(mod 60)是不可解的。
又如3(mod 6)≡r(mod 9)中,r只能是0,3或6,故知方程3(mod 6)≡1(mod 9)是不可解的。很明显,方程3(mod 6)≡2(mod 8)也是不可解的。因为前边余数是奇数,而后面则是偶数。
看来,哥庭根抄本所论不定分析问题,对模数两两互素的情况,其解法只适合于较小的数,对非两两互素的情况,作者未必十分了解一般可解的条件。
