10.3.2 物不知数题在西方的历程
中国不定分析史料在西方的历程是数学史上一个重要的课题[4]。
李俨[5]最早简略提及马蒂生、康托、三上义夫和赫师慎的工作。
近年，杨琼茹[6]详尽收集东西方相关史料，增加了朝鲜数学家庆善征（1616—？）、黄胤锡（1729—1791）的内容，有力地推动了这个课题的研究。
在欧洲，和秦九韶同时代的意大利数学家斐波那契[7]，在《计算之书》（1202年）中给出了两个一次同余问题，从形式到数据，都和物不知数题相仿。
1734年，欧拉研究了不定方程和一次同余式组的解法。
1801年，高斯写下《算术研究》，完善了同余理论。
秦九韶解一次同余式组的大衍求一术为西方学者所理解，并不是一件容易的事。
19世纪上半叶以前，西方学者对中国数学知之甚少。
法国著名数学史家蒙图克拉（Montucla，J.E.，1725—1799），在其数学史经典著作《数学史》第一卷第二部分第四章，专论中国数学史。蒙图克拉所能见到的，只有18世纪来华耶稣会士宋君荣（Gaubil，A.，1689—1759）等关于中国天文学的著述。此章虽名为“中国数学史”，实际上主要是对中国天文学的介绍。此后半个世纪，蒙图克拉的著作以及耶稣会士的有关著述，成了西方学者了解中国数学的主要文献。
1839年3月毕瓯（Biot，E.，1803—1850）在《亚洲杂志》（Journal Asiatique）上发表了十二卷本《算法统宗全书总目》。在卷五最后，毕瓯介绍了《孙子算经》的物不知数题，但没有给出解法。
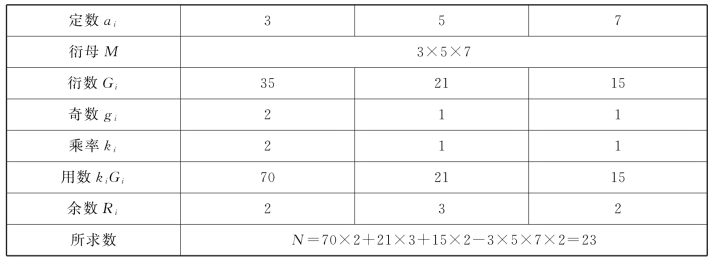
1852年英国传教士伟烈亚力[8]（Wylie，A.，1815—1887）为纠正西方学者的错误看法，在上海英文周报《北华捷报》上发表中国数学科学札记，用秦九韶大衍术介绍《孙子算经》物不知数题解法（表10.2），但未能具体介绍求乘率的求一术。
表10.2 解物不知数题
解法中，两个奇都是1，直接取乘率。另一个奇为2，伟烈亚力只介绍说：“然后将这个大于1的奇用于一个称作‘求一’的辅助过程：衍母和奇辗转相除，直到余数化为1。本例中得数为2，即为乘率。”但根本没有说清乘率是怎样求得的。
伟烈亚力又全文翻译了《数书九章》大衍类第1题蓍卦发微的解法，不过同样没有交代求乘率的方法。除翻译古历会积、余米推数两题题文外，泛泛介绍了其他题目。
此外，伟烈亚力误认为，一行最早应用大衍术于《大衍历》，导致谬种流传。
德国学者毕尔那茨基（Biernatzki，K.L.）在柏林偶然看到了伟烈亚力的论文，将其译为德文，但做了许多改动，于1856年以中国之算术为题发表。
1874年，德国数学家马蒂生[9]（Mathiessen，L.，1830—1906）在给康托的一封信里，纠正了毕尔那茨基的错误，并证明：中国的大衍术与德国大数学家高斯的解法是等价的。
1881年，马蒂生又撰文论述大衍术，以现代记号表示剩余问题的解法（表10.3）。马蒂生给出高斯解法，说明它与中国解法的一致性，并指出其中的α，β和γ，即为秦九韶的“用数”。
文中介绍了物不知数题（表10.3）。
表10.3 物不知数题解法
N=2×2×5×7+3×1×3×7+2×1×3×5-3×5×7n=233-105n。
由于马蒂生只看过毕尔那茨基的译文，而无任何其他文献可依，因此，他错误地把秦九韶当成是公元4世纪《孙子算经》和唐开元十七年（公元729年）《大衍历》的注者。
一个德国学者马蒂生，在他那个年代，利用1801年的高斯《算术研究》，分析1247年的秦九韶大衍总数术，求解4世纪《孙子算经》的物不知数题，时空跨度巨大。这位东西方不定分析史研究的先驱，开垦草莽，居功至伟，更鞭策今天的人们研究秦九韶、高斯原文、原术、原意，挖掘历法史料，深入东西方比较数学史的广阔领域中去。