11.4 序列线性组合定理
若a和b是不定方程ax=by±1的两个系数，a，b是正整数，a不小于b。由可解条件，a与b互素。于是，互素整数对所求出的自然余数与调节余数，均为1。
现在，我们单独讨论序列线性组合定理，不采用商数损一调节举措。
序列线性组合定理[5]
其中，
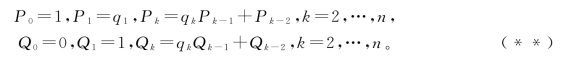
证明 我们把序列组合用余数表示，再用归纳法进行证明。
（1）当k=1时，（*）式为Q1a-P1b=（-1）0r1=r1。
由初始值Q1=1，P1=q1，有a-q1b=r1，即第一步除法a=q1b+r1，（*）式成立。
（2）当k=2时，由初始值P0=1，P1=q1和Q0=0，Q1=1，有Pk=qkPk-1+Pk-2成为P2=q2P1+P0=q2q1+1，Qk=qkQk-1+Qk-2成为Q2=q2Q1+Q0=q2×1+0。
代入（*）式，有
Q2a-P2b=(q2×1+0)a-(q2q1+1)b=q2a-(q2q1+1)b=aq2-b-bq1q2
=q2(a-bq1)-b=q2r1-b=-r2=(-1)2-1r2。
其中，第五个等号利用第一次除法r1=a-q1b，第六个等号利用第二次除法r2=b-q2r1。
下面应用归纳法。
假定式（*）和（**）对k＞2的正整数k成立，考察k-1，k，k+1三种情况：
对k-1，式（*）有Qk-1a-Pk-1b=（-1）k-1-1rk-1=（-1）k-2rk-1，即（-1）k-2·（Qk-1a-Pk-1b）=rk-1。
对k，式（*）有Qka-Pkb=（-1）k-1rk，即（-1）k-1（Qka-Pkb）=rk。
对k+1，式（**）有Pk+1=qk+1Pk+Pk-1和Qk+1=qk+1Qk+Qk-1。
现需证Qk+1a-Pk+1b=（-1）k-1+1rk+1。
对k+1，把辗转相除第k步
rk-1=rkqk+1+rk+1
移项，再两边乘（-1）k，有
(-1)krk+1=(-1)k(rk-1-qk+1rk)
=(-1)k[(-1)k-2(Qk-1a-Pk-1b)-qk+1(-1)k-1(Qka-Pkb)]
=(-1)2k-2(Qk-1a-Pk-1b)-qk+1(-1)2k-1(Qka-Pkb)
=(Qk-1a-Pk-1b)+(-1)(-1)qk+1(Qka-Pkb)
=(Qk-1a-Pk-1b)+qk+1(Qka-Pkb)
=(qk+1Qk+Qk-1)a-(qk+1Pk+Pk-1)b
=Qk+1a-Pk+1b。
其中，第二步的代入，根据两个归纳假定。第三步演算（-1）2k-2=1，第四步演算（-1）2=1。最后一步，依据Pk+1=qk+1Pk+Pk-1和Qk+1=qk+1Qk+Qk-1。
由归纳法，定理成立。
采用了商数损一调节举措的辗转相除过程，有如下规定（表11.4）：
表11.4 商数损一调节举措
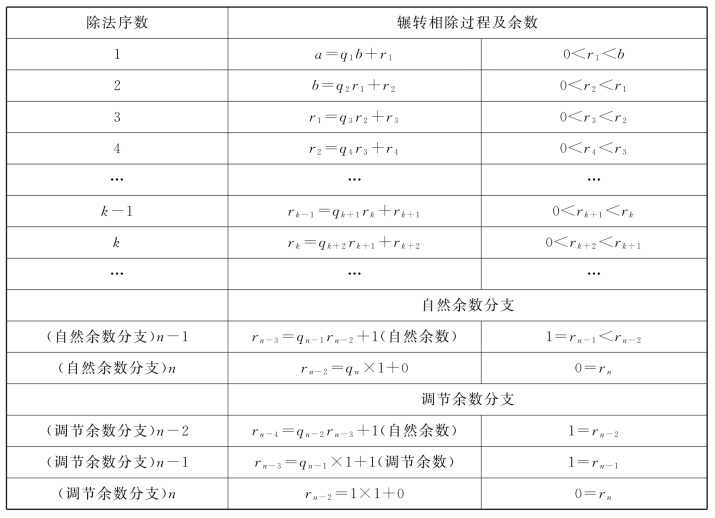
表11.4中，调节余数分支中的自然余数为1，就是自然余数分支中的自然余数为1。