16.7.4 构思探索
探索刘歆引入上元积年的具体原因和构思细节，困难重重。
1928年日本学者新城新藏[24]开垦草莽，以31个元试算，以线性四元不定方程进行推测。
1980年李文林、袁向东[25]推测，推算三统上元之关键，是汉历太初元年……前十一月甲子朔旦冬至。刘歆编造“岁星超辰”，三统历“岁术”以岁星一百四十四年而超一次，即一百四十四年行一百四十五次。可把岁在星纪婺女六度，理解成处于30度星纪的
，r在135与139之间。
如果以p，q为不定整数，q为岁星运行圈数，有线性不定方程：
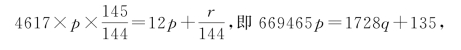
相当于以x为未知数的线性同余式：
仅当余数r取整数135，即有
时，有最小正整数解x=31。由此可算出上元积年数4617×31=143127。
前辈们不畏艰难，披荆斩棘，开阔了我们的视野，鞭策着我们一步步前进。
现在我们要解答，这个135是怎样取得的？
探索可分5步，每一步都有史料上的依据。
1 落下闳的密近简化
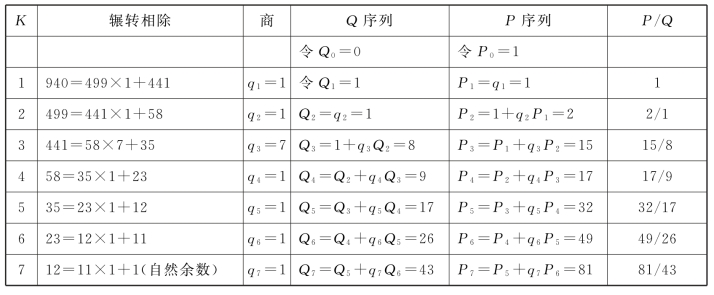
我们赞成吕子方对落下闳日法81来源的推测，只是把连分数之说换成等价的密近简化。落下闳以古六历
作源，用密近简化法试算出太初历的
序列值计算表如下（表16.6）：
表16.6 940和499序列值计算表
汉代对音律的认识，主要是三分损益律。太初历历法数值基本都与3有关。
如《汉书》所载：“闳运算转历，其法以律起历”，落下闳选用3的倍数81。
整数对现象各值体现的内在数理关系，使得人们可以根据某一个特征，作为关联另一个特征的标志，导出所需结论。
分子、分母各为三位的499与940，比值为0.530851。分子、分母各为两位的43与81，比值为0.530864。精确到小数点后第六位，两者相差0.000013。如果要作为日法，构建起历法整数论，81更适宜于历法的编制。
围绕太初历日法81，我们无法提供进一步的史料。但判断落下闳知晓密近简化术，应该是有把握的。
2 等数用于关联
刘歆熟知落下闳把940，499密近简化为81，43的计算过程。
同时代的《九章算术》描述过更相减损术，引出关键概念等数。
当然，以更相减损作术名的，只是求等数术减法形式。现存史料上未曾见到单独的求等数除法形式。但删除1208年原筹算图左列，右列上下，就是传统数学的求等数除法形式。
我们认为，刘歆沿用前人的求等数除法形式，落下闳就曾用来进行密近简化。
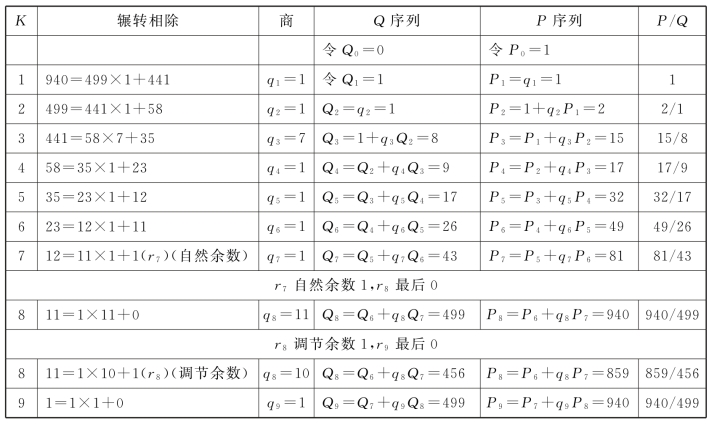
在940和499序列值计算表（表16.7）中，算到除法12=11×1+1（r7）（自然余数）。再算下一步，是11=1×10+1（r8）（调节余数）。筹算板上下，1（r8）=1（r7），合称等数。
刘歆的突出贡献，是引入两个余数1组成的等数1作为标志，用来关联81与43。
表16.7 940和499序列值计算表扩展
3 满去式的解
太初元值4167岁的31倍，即太初上元值143127，衔接起太初历与三统历。
汉历太初元年，距上元十四万三千一百二十七岁。前十一月甲子朔旦冬至，岁在星纪婺女六度，故《汉志》曰：岁名困敦，正月岁星出婺女。
从上元起，31个元，即143127岁，按岁术可有“岁在星纪婺女六度”，恰与《汉志》“正月岁星出婺女”相符。此举对三统历体现天人感应权威意义极大。“故《汉志》曰”的“故”字，显露着2000多年前刘歆的得意之情。
刘歆可能是在大量计算时，偶遇31这个值，启发思想升华，反转条件与结论。谋求用数值解法，利用元4617岁和“婺女六度”，反推算出值31。
进而探索元数数值计算。这相当于考虑现今所说的线性同余式问题：
岁星超辰运行，从上元起历经多少个元4617岁，到太初元年岁首处于“星纪婺女六度”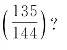
我们赞成李文林、袁向东推测中的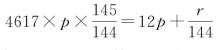
，即669465p=1728q+135，或669465x≡135（mod 1728）。我们只是想换成等价的满去式：多少个669465，满去1728，不满135？
4 筹算模仿
模仿开禧历大衍术筹算图，计算669465与1728，见表16.8。我们看到：相等的27合为等数，标志左上19为乘率。
顶行表示辗转相除关系，第二行突出当前筹算操作目标，底下一行标筹算图序号。
表16.8 模仿1208年筹算图计算669465与1728
图9除法81=27×2（q6）+27（r6），由商数损一调节，商（q6）取2不取3，产生余数27（r6）。图10上下27各标一个等字。到图11，两个相等的27才合为等数，标志左上19为乘率。
这里，自然余数27（r5）除法序数5为奇，单独的等数自然值27（r5），本来就是取自然余数分支序列值的充分必要条件。然而，为了追求等数，画蛇添足，必凑等数调节值（r6）27，必闯调节余数分支，必误求图11左下（Q6）45（调节余数分支序列值），并冲击右列上下轮流作被除数的规律，从而陷入陷阱。
然而，传统历法的求乘率术，以等数检测乘率，直观简单。适用于奇序、偶序一切整数对，都能求出乘率，足以支撑中华文明千年传统历法的辉煌[26]。
5 最小正整数解
整数对669465与1728入大衍术，与约简的整数对24795与64入大衍术，乘率都是19。这是涉及整数对现象的既约分数问题。
求解多少个669465，满去1728，不满135，可用开禧历求入元岁之术理，原文如下：
又以日法乘前历所测冬至气刻分，收弃末位为偶数，得斗分，与日法用大衍术入之，求等数、因率、蔀率，以纪乘等数为约率，置所求气定骨，如约率而一，得数，以乘因率，满蔀率去之，不满，以纪法乘之，为入元岁。
模仿算图中算出等数27、因（乘）率19。开禧历的纪（纪法）源于干支周期60。此处纪（纪法）为1，约率等于等数27。约135得5，约1728得64。
核算：669465×31=20753415，20753415-135=20753280，20753280=1728×20753145。
31是最小正整数解，正是从太初元跨越到三统上元积年的核心，说明刘歆对满去式的最小正整数解概念是有所了解的。
大量试算中的偶然发现，碰撞到数理的内在逻辑擦出的火花，引导刘歆求解线性满去式，成为上元积年计算第一人。闯入这个数学领域的刘歆，不会透彻了解其间数理，并未明确意识19为乘率。从乘率19到最小正整数解31还需要关键一步。以乘率19乘5得95。95已是669465x≡135（mod 1728）的解。以95满去64所得的31则是最小正整数解。
然而，所面临正反核算问题，以特定数值关系探索，还是能够解决的。