14.13.4 借数转移
推库额钱题和积尺寻源题中，尝试了第二种调用数法：“至多处借之”。与上面的“损去部分衍母”类似，根据元数，先验同类，再转换成“几约如意”，转移借数。
总数术中说：
或定母得一，而衍数同衍母者，为无用数，当验元数同类者，而正用至多处借之。以元数两位求等，以等约衍母为借数，以借数损有以益其无，为正用。
或数处无者，如意立数为母，约衍母，所得以如意子乘之，均借补之。
或欲从省勿借，任之为空，可也。
“如意立数”之举是秦九韶的盲目扩大化，“从省勿借”则是事实的描述。
关于借数的内容，涉及推库额钱题。算草中有这样一段描述无衍数：
次验诸衍数，有同衍母者，皆去之，为无衍数。
以两行对乘之，为用数，甲无，……，庚无。
甲、庚衍数27720，与衍母27720相同，称无衍数，记为0。奇数与衍数相乘，称无用数，也记为0。
算草后面一段描述借数的移动：
次以推无用数者，惟甲庚合于同类处借之，其同类谓元陌列而视之。
今视甲12，庚6，皆与丙10，戊8，俱偶，为同类。其戊用数3465，其数少，不可借，唯丙10之用数，系22176，为最多，当以借之，乃以甲12，丙10，庚6，求等得2，以等数2，约衍母27720，得13860，为借数，乃减丙用22176，余8316，为丙用数，乃以所借出之数13860为实，以元等2为法，除之，得6930，为甲用数，以甲用数减借出数，余亦得6930，为庚用数，今不欲使甲庚之借数同，乃验借出数13860，可用几约如意，乃立3，取三分之一，得4620，为甲用，取三分之二，得9240，为庚用，列右行。
我们摘录出相关表格（表14.26），括号标注相关数值的性质：
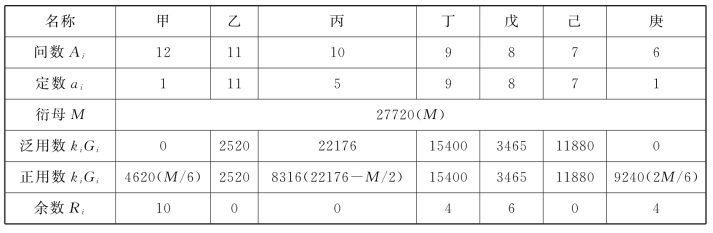
表14.26 推库额钱题调用数
验甲12、庚6、丙10、戊8为偶数，同类，戊用数3465最小，丙用数22176最多。求总数：
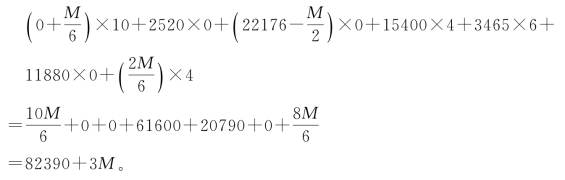
调用数前、后，用衍母27720（M）除，都能得到26950，全仗余数的巧合。
还有一个是积尺寻源题。算草中有这样一段，用括号标记其与衍母的关系：
凡诸用数同类者，数必多，可互借以补无者。先验革元数25与木元数20为同类，求等得5，以等5约衍母85800（M），得17160（M/5），乃于革用数（61776）内减出，以补木位，为木用，余44616，为革用。次验竹元数100与土50为同类，以求等得50，以等50约衍母85800（M），得1716（M/50），亦于革用内各借与竹土为用数，革止余41184为用，得诸定用数。
我们摘录出相关表格（表14.27），括号标注相关数值的性质：
表14.27 积尺寻源题调用数
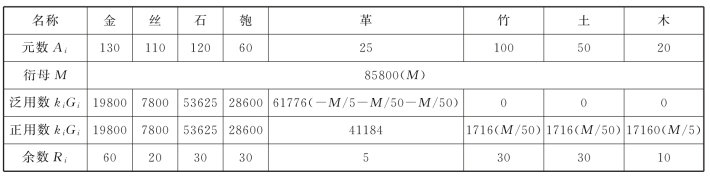
先用具体数据计算一下。不调用数之前，得1230。
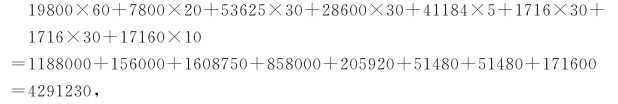
4291230满去85800，不满，广为1230。
调用数方法是革25与木20元数同类，等数5约衍母，得17160（M/5）。从革用数61776移动至木用数，得44616和17160。竹100与土50元数同类，以等50约衍母，得1716（M/50）。再从革用数44616中扣除，得41184。
用数乘余数，求总数时，我们不考虑金、丝、石、匏四项，只看移动相关的革、竹、土、木四项。61776扣除17160（M/5）得44616，再扣除两个1716（M/50）得41184。
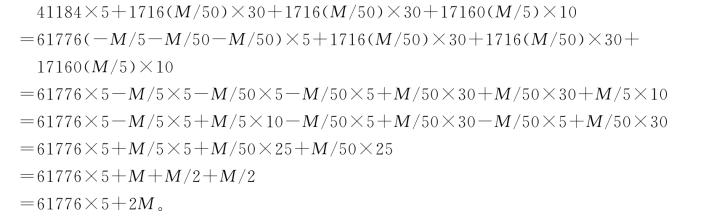
这样，在如术文“满衍母去之，不满，得广深”操作中，移动相关的革、竹、土、木四项，在调用数之前，与调用数之后，所得广深数据是一样的。