14.15 大衍求一术诞生探索
秦九韶在《数书九章·序》中,自称:“早岁侍亲中都,因得访习于太史,又尝从隐君子受数学。”
1208年开禧历所存求乘率术筹算原图操作,不知何人何时所定。不要说今天的人们不习惯,就是中世纪的秦九韶,也痛感不便。
秦九韶亲手设计1247年元闰朔率求乘率图,为每一个数值的布图费尽心机,也就有可能受到启示,逐步改进。参见图11.2“1247年秦九韶改良的大衍图”。
我们展示从元闰朔率求乘率图结构,演变到大衍求一术的可能过程[21]。
先删除原来双数的2,4,…,20十图,只用括号的数字表示,保留单数原图。形成下列算图(图14.5)。
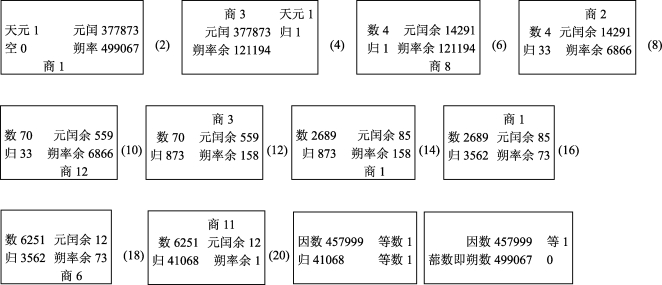
图14.5 删除双数图的大衍图
接着,略去注文,把商数移到两图之间,形成下列简图(图14.6):

图14.6 改良大衍图的简图(https://www.daowen.com)
有趣的是,包括首尾在内的每一张筹算小图,右上角和左下角相乘的积,加上右下角和左上角相乘的积,其和恰好都等于恒值,即首图右下角的数,也是尾图左下角的数。这个对角线乘积和的恒等性质,是数理与算筹摆法的奇妙结合。
我们在13.9.3“等数只是充分条件”中指出:等数是辗转相除过程中两个相等的余数,只是标志乘率的充分条件。只有处在右上位的等数自然值(或等数调节值)单独一个,才具有标志乘率的效力。
秦九韶工作中最重大的突破性贡献,就是把等数作乘率标志,改为以右上余数1作乘率标志,也就是只用了真正能标志乘率的那个等数自然值(或等数调节值)。在前人基础上,模仿设计求乘率图、简化排图,最后以简练的语言归纳出大衍求一术。
1247年大衍求一术原文如下:
诸衍数,各满定母去之,不满曰奇。以奇与定,用大衍求一入之,以求乘率[或奇得一者,便为乘率]。
大衍求一术云,置奇右上,定居右下,立天元一于左上。先以右上除右下,所得商数,与左上一相生,入左下。然后乃以右行上下,以少除多,递互除之,所得商数,随即递互累乘,归左行上下。须使右上末后奇一而止。乃验左上所得,以为乘率。或奇数已见单一者,便为乘率。
秦九韶回避首图的0,也回避最后0这个麻烦,以“右上末后奇一”准确地选定具有乘率标志效力的余数1。取消商数,略去最后一图。所有筹算图与大衍求一术术文的描述完全一致,体现出这样的数理含义:以除法为纲,把同一个循环的试商、留余、归算并入同一个算图。
秦九韶具有极高的数学造诣,归纳提炼的大衍求一术“整个算法几乎可以一字不差地搬到现代电子计算器上去实现”[22]。
秦九韶万世流芳,在伟大数学家高斯之前554年得到的大衍求一术,与线性不定方程现代序列解定理等价,而不定方程序列解法正是高斯同余式算法的核心。
至此,等数完成了标记乘率的阶段性历史使命。秦九韶的元数格说:“元数者,先以两两连环求等,约奇弗约偶。”等数回到求等相约过程中,重操最大公约数的老本行。
