11.7.3 经典研究中的原字母
1921年8月,钱宝琮写《求一术源流考》一文,1925年写《商余求原法》[7]一文,1966年再写《秦九韶数书九章研究》[8]一文。在中国数学史研究上,钱宝琮第一个系统、完整研究了大衍求一术的数学证明,作出了不可磨灭的贡献,成为后世学者的楷模。
这些经典研究中,大衍总数术的符号:定数ai、衍母M、奇数gi、乘率ki、用数kiGi、余数Ri、各总kiGiRi、解N等,始终保持不变。仅序列字母前后略异。有必要把“秦九韶数书九章研究”一文的原文、原字母,照录如下:
如果G>a,设G≡g(mod a),0<g<a,则同余式kg≡1(mod a)(2)式与kG≡1(mod a)(1)式等价。式内的g称为奇数。
大衍求一术云,置奇右上,定居右下,立天元一于左上。先以右上除右下,所得商数,与左上一相生,入左下。然后乃以右行上下,以少除多,递互除之,所得商数,随即递互累乘,归左行上下。须使右上末后奇一而止。乃验左上所得,以为乘率。
用代数符号说明大衍求一术如下:
以g,a二数辗转相除,得到一连串的商数q1,q2,…,qn,到第n次的余数rn=1而止,但n必须是个偶数。如果rn已经等于1,那么以1除rn-1得商qn=rn-2-1,余数rn还是1。与辗转相除同时,按照一定的程序,依次计算c1,c2,…,cn:
a=gq1+r1,c1=q1,
g=r1q2+r2,c2=q2c1+1,
r1=r2q3+r3,c3=q3c2+c1,
︙
rn-2=rn-1qn+rn,cn=qncn-1+cn-2。
最后得到的cn就是k值。我们可以证明这个方法的正确性。设l2=q2,l3=q3l2+1,l4=q4l3+l3,…,ln=qnln-1+ln-2,从上面(3)式里,我们有
r1=a-gq1=a-c1g,
r2=g-r1q2=g-(a-c1g)q2=(1+c1q2)g-aq2=c2g-l2a,
r3=r1-r2q3=(a-c1g)-(c2g-l2a)q3=(1+l2q3)a-(c1+l2q3)g=l3a-c3g,
︙
rn-1=ln-1a-cn-1g,
rn=(-1)n(cng-lna)。
也就是
cng≡(-1)nrn(mod a)。(https://www.daowen.com)
当rn=1时,k=cn。我们有kg≡1(mod a)。
上面求k值的方法和初等数学书中解一次不定方程gx=ay+1的方法差不多,只是k=cn是从q1顺次算到qn止所得的,而x是从qn算起逆推到q1止所得的结果。x=k(mod a)是可以证明的。
例如,在推计地功题的演算过程中,需要计算满足同余式3800k≡1(mod 27)的k倍。因3800≡20(mod 27),故以20为奇数,27为定数,以奇与定入大衍求一术求乘率如下:
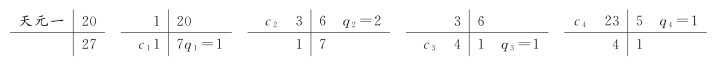
因得3800×23≡1(mod 27)。
这里顺便作一个注。介绍求一术时,“作十字号以界之”[9]。李俨先生认为乃是比利时来华传教士赫师慎(Van Hee L.,1873—1951)的发明,又认为他对大衍求一术的介绍比三上义夫更为详细。汪晓勤[10]则认为:“这是不符合事实的。”
注意,此处使用的单序列c1=q1,c2=q2c1+1,c3=q3c2+c3,…,cn=qncn-1+cn-2,所得到cn就是k值。证明中设了另一单序列l2=q2,l3=q3l2+1,l4=q4l3+l2,…,ln=qnln-1+ln-2。
这种c序列、l序列与Q序列、P序列的关系,用具体数字例子即可查明。
现在按“奇定处大衍求一术”,定a=gq1+r1,c1=q1,奇g=r1q2+r2,c2=q2c1+1,…,用27和20的序列值计算(表11.11)。
表11.11 27和20的序列值计算

续表
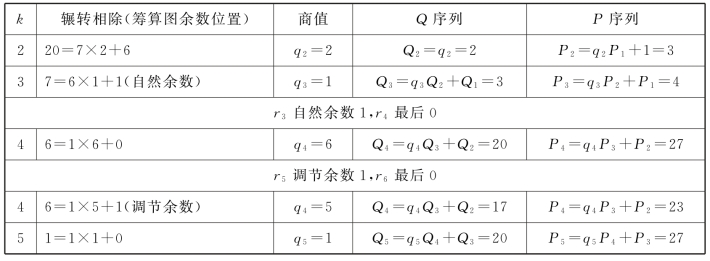
自然余数1(q3)对应的序列值3(Q3)和4(P4),x=3和y=4是27x=20y+1的一组解。核算:27×3-20×4=1。
调节余数1(q4)对应的序列值17(Q4)和23(P4),x=17和y=23是27x=20y-1的一组解。核算:27×17-20×23=-1。
注意,调节余数1(q4)对应的23(P4),除法序数4正是偶数,符合“以g,a二数辗转相除,得到一连串的商数q1,q2,…,qn,到第n次的余数rn=1而止,但n必须是个偶数”。
可见此处,大衍求一术中用单个P序列表示为cn,不是Q序列。天元一是P1。列出的大衍求一图应当如图11.4所示。
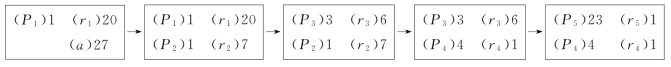
图11.4 偶序整数对的大衍求一图
至于这一句:“上面求k值的方法和初等数学书中解一次不定方程gx=ay+1的方法差不多,只是k=cn是从q1顺次算到qn止所得的,而x是从qn算起逆推到q1止所得的结果。x=k(mod a)是可以证明的。”我们只需要确认一下,“顺次”指上面的方法,而“逆推”则指解不定方程gx=ay+1的回代方法。
