11.7.1　奇序整数对

在开禧历求乘率原图中，我们约去52，取奇序整数对118704，325，用序列值解法（表11.7）。

表11.7　118704和325序列值计算表

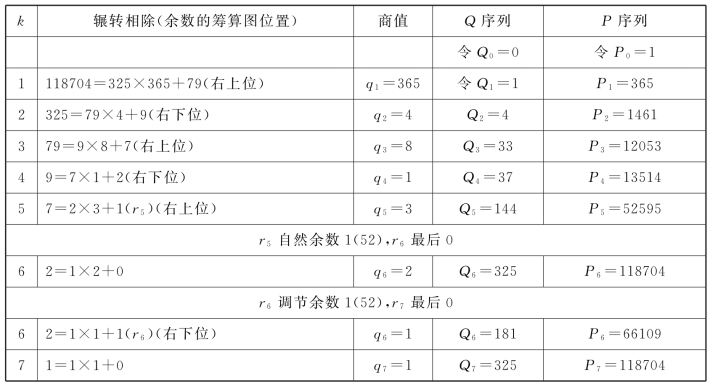
自然余数1（r5）在右上位，所对应的序列值是Q5=144，P5=52595。知x=144和y=52595为常数1不定方程118704x=325y+1的一组特解。144是同余式118704x≡1（mod 325）的特解。核算：118704×144=325×52595+1（表11.8）。

开禧历将144称为乘率。可解出满去式：多少个6172608，满去16900，不满为62？

调节余数1（r6）在右下位，所对应的序列值是Q6=181，P5=66109。知x=181和y=66109，为常数1不定方程118704x=325y-1的一组特解。181是同余式118704x≡-1（mod 325）的特解。核算：118704×181=325×66109-1（表11.8）。

表11.8　奇序整数对与两种不定方程的可能解

1874年，黄宗宪称144为整数对118704和325的乘率，将181称为整数对118704和325的反乘率。我们可以验算，144是乘率：118704×144-325×52595=1；181是反乘率：118704×181-325×66109=-1。