2.6　具体细节

李文林、袁向东推测，推算三统上元之关键，是“汉历太初元年……前十一月甲子朔旦冬至，岁在星纪婺女六度”。假设从三统历元到太初元年的积年数为N，应是一元4617的倍数，记作p，即

N=4617×p（p为整数）。

为了进一步推算p值，需要利用“岁在星纪婺女六度”。

中国古代使用岁星纪年，岁星即木星，最早测得其十二年一周天，故分周天为十二次，岁星每年行一次，并以它所到之次作为岁名，如“岁在星纪”，就是这一个岁星行至“星纪”这一次。后来发现岁星周期实际比十二年短，遂有“超辰纪年”。三统历“岁术”以岁星一百四十四年而超一次，即一百四十四年行一百四十五次。

由此，在N=4617×p年内，岁星运行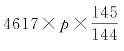次，而止于星纪婺女六度，故以12除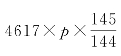，所得余数应恰好与“岁在星纪婺女六度”相符合。

这句话，理解成处于30度星纪的，r在135与139之间，可推得一次不定方程：

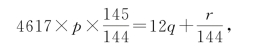
即

4617×145×p=1728×q+r,

相当于一次同余式4617×145×p≡r（mod 1728），这里p，q为不定正整数，q为岁星运行的圈数。r虽未完全确定，但有个范围135≤r≤139。在此范围内，仅当r=135时，有整数解，且最小正整数解p=31，此时，N=4617×31=143127，恰为《世经》所载三统上元积年数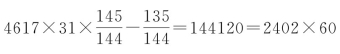，恰为60的整倍数，故三统上元，按超辰干支纪年，岁名应与太初元年相同，俱为丙子。

李文林、袁向东指出，汉历上元积年推算中，余数r的选择恰好都符合可解性条件，这应该说不是偶然的。至于说，汉代历算家究竟解一次不定方程还是一次同余式，具体方法是什么，都不能凭空臆断。从p和q两者在公式中的地位看来，后者的值无关紧要，只要前者即可推算出上元积年，因此，很可能一开始就当作一次同余式来处理，并且不排斥对于单个一次同余式用更相减损法辗转相除求解。