15.4.3　骆腾凤的大衍奇定相求法

骆腾凤（1770—1842），字鸣冈，号春池，江苏山阳人。《艺游录》二卷（1815年）中求乘率的大衍奇定相求法，原文[20]如下：

大衍求一术云，置奇右上，定居右下，立天元一于左上。先以右行上下两位，以少除多，所得商数，乃递互乘归左行，使右行末后奇一而止。乃验左行所得，以为乘率。

凡大衍求一法，先列一奇元于左，空定元于中，正奇数于右，在上位。次列空奇元于左，一定元于中，负定数于右，在下位。其理为：一奇元比空定元多奇数，空奇元比一定元少定数也。凡奇命为正，定命为负，奇余恒得正，定余恒得负。

以定母除衍数，不满法者为奇，是奇恒少于定也。法以奇数商除定数，定必有余，故第一次即以商除数乘一奇元、空定元、正奇数，而与空奇元、一定元、负定数相减[奇元、定元以加为减]，则得几奇元比一定元少定余数。

今按照骆腾凤的大衍奇定相求法演算（图15.3）。算图中正负号及旁注均系我们依意加入，引号中为原文，横线则依原文。

3800满27去之，不满20为奇，27为定。“凡奇命为正，定命为负，奇余恒得正，定余恒得负。”

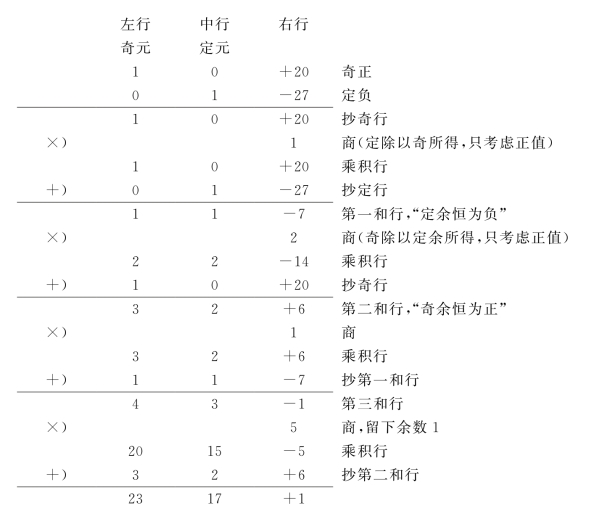
图15.3　骆腾凤的大衍奇定相求法演算

我们可以验算：23×20-17×27=1。