12.3.2 高斯的辗转相除
约定a和b来源于ax+by=±1，a，b是正数，不妨假定a不小于b。我们简称为大系数项ax约定。由可解条件知a，b互素，自然余数为1。
任何线性不定方程都能通过移项、字母转换等措施，满足大系数项ax约定。
附有商数损一调节举措的辗转相除过程，是第二段。
由商数损一调节，展示自然余数1和调节余数1，最后得到入算互素整数对重现。
现在我们考虑不定方程ax=by±1，a，b是正数，不妨假定a不小于b。现在通过求两个数最大公约数的已知算法，用普通除法构成等式
a=αb+c，b=βc+d，c=γd+e，等等，
使得α，β，γ等，c，d，e等是正整数，数值递降，直到m=μn+1，这总是可以做到的，结果会是
a=[n,μ,…,γ,β,α],b=[n,μ,…,γ,β]。
所谓“已知算法”，指余数为0的现代欧几里得辗转相除法。“m=μn+1，这总是可以做到的”，说的是应用商数损一调节举措，形成自然余数1和调节余数1，伴有各自的商μ、被除数m和除数n。这里的除数n与对应于余数0的商n，字母相同，含义不同。
一般而言，由a=[n，μ，…，α]表示，商系列记α，…，μ，n。商n对应于余数0。
互素奇序整数对118704和325序列值计算如下表（表12.1）。
表12.1 互素奇序整数对118704和325序列值计算
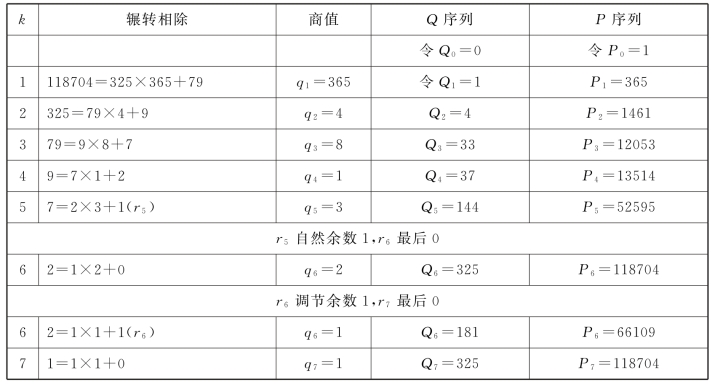
表12.1中，118704与325互素，除法7=2×3+1产生自然余数1（r5），商3损1为2，于是除法2=1×1+1（r6）产生调节余数1（r6）。两个余数连同各自后续的0，组成两个余数分支。
余数0相关序列值“a=[n，μ，…，γ，β，α]，b=[n，μ，…，γ，β]”，重现互素入算数。
表中，自然余数分支结尾，对应r6=0，325（Q6）=325（b）和118704（P6）=118704（a）。调节余数分支结尾，对应r7=0，325（Q7）=325（b）和118704（P7）=118704（a）。