15.5.3　一次同余式组的解

15.5.3　一次同余式组的解

第二卷中，黄宗宪“反乘率”“新术”共分两段，均带有按语。变量并没有用任何现代数论符号表示，而是用清代流行的干支符号来表示。每当新定义一个量，加圆圈标出，第二次、第三次使用子程序时，有关量正上方分别加两撇、三撇，以示区别。

现在为排版本文的方便，改用圆括号代替圆圈，把两撇、三撇加在有关量的右上角。

方括号中为原文小字注。

术曰：先取题中减数最大者命为（甲），其本位剩数为（子）。又取略小于甲之减数为（乙），其本位剩数为（丑）。

从整个定理的角度看，他首先考虑前两个模和它们的余数，把所有的问数作降幂排列：

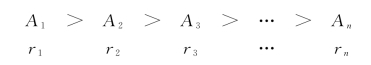
接着，他提出只处理两个模的子程序：

乃以甲乙求等，以等约乙[无等不约。或以等约乙，得数，与甲仍有等者，则用析根法求之。后仿此]。

黄宗宪介绍解法如下：

甲乙相乘得（甲′），以乙累减子，余（丙）。又以乙累减甲，余（丁）。于丙内减去一丑[不足减者，加一乙以减之。下同]，余（戊）。

以乙[比定母]丁[比衍数]对列两行，求得反乘率。以乘戊，得（己）。甲己相乘，得（庚）。并子庚，得（辛）。以甲′累减辛，余（子′）。[以上为一次求法。]

解的后面，还加了两个注：

按凡题中有三次减数者，其求法有二次；有四次减数者，其求法有三次。以后减数每增一次，其求法亦每增一次。

按其三次四次以往，仿此求之。唯叠次各干支字上，多加一′为识耳。

这些句子表明，黄宗宪用（n-1）次子程序去处理n个一次同余式。

注的后面有三个数例，反映了前面所讲的内容。