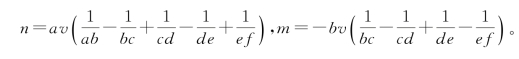9.2.1 形如ma+v=nb的不定方程
狄克逊的《数论史》中这样记录:
欧拉给出了一个寻找整数m的过程,使得(ma+v)/b是一个整数,这里v>0。设a=αb+c,于是A=(mc+v)/b必须是个整数,从而有m=(Abv)/c。
首先,如果v可被c整除,我们取A=0,得到一个解。其次,如果v不能被c整除,设b=βc+d。那么如果(Ab-v)/c是个整数,m会是个整数。这样我们设c=γd+e,等等。
欧拉给了一个注,称这个过程是寻找a,b最大公因数的过程,继续进行,直到得到一个能整除v的余数。他解ma+v=nb的公式等价于
![]()
这个级数继续进行,直到找到一个能整除v的余数。
欧拉解形如ma+v=nb的不定方程,m和n是两个变量,a和b分别是m和n的系数,v是常量,不失一般性,要求v>0。
把a,b辗转相除,求出一系列余数c,d,e,f,…,直到余数f能整除常量v为止。直接得到不定方程的一组解m和n:
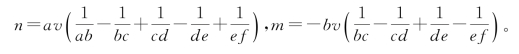
括号中均是级数,两级数的最后一项![]() 取决于能整除v的余数f。
取决于能整除v的余数f。
我们分析整个过程:
如果原不定方程有整数解m和n,则因整数![]() ,就有
,就有![]() 为整数。设有除法a=αb+c,α是商数,c是余数。代入
为整数。设有除法a=αb+c,α是商数,c是余数。代入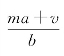 ,得
,得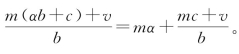 。形式分数部分
。形式分数部分![]() 记为A,实质为整数,则有
记为A,实质为整数,则有![]() 。因m是整数
。因m是整数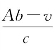 应该是整数。(https://www.daowen.com)
应该是整数。(https://www.daowen.com)
这就是说,原不定方程能否有整数解,取决于v与c整除与不整除两种可能。
整除 如果v可被余数c整除,取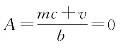 ,得到
,得到
m=-v/c。
于是,前述的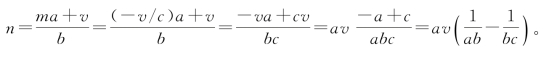
这是找到了能整除v的余数c,就会出现表示m和n的两个级数。这就是说,如果v可被余数c整除,则形式分数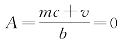 ,体现出实质上的整数。
,体现出实质上的整数。
不整除 如果v不被余数c整除,设除法b=βc+d,β是商数,d是余数。记B为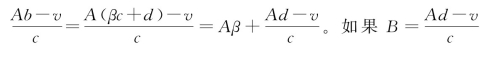 为整数,可知
为整数,可知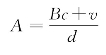 为整数。
为整数。
到这一层里,原不定方程能否有整数解,取决于v与d之间整除不整除两种可能。
整除 现在设v能被d整除。取![]() 。有
。有
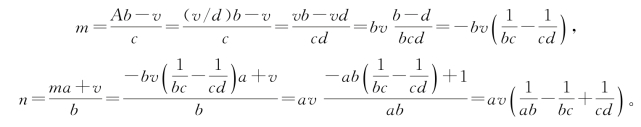
不整除 如果v不能被d整除,再进行类似上述的计算。
由此可知,a,b辗转相除,求出余数c,d,e,f,…。假设某个余数f能整除常量v,可得不定方程的一组解m和n: