14.13.2　多一者为正用

14.13.2　多一者为正用

秦九韶在孙子剩余定理中发现了一个涉及用数的性质：

k1G1+k2G2+…+knGn≡1(mod M)。

在大衍总数术中，有明确记录：

置各乘率[ki]，对乘衍数[Gi]，得泛用[kiGi]。并泛[kiGi]课衍母[M]，多一者为正用[kiGi]。

泛用指尚未调节的用数，正用指最终确定的用数。

我们把孙子定理表示为一般形式：

设有数N被n个两两互素的a1，a2，…，an除，所得余数分别为R1，R2，…，Rn。

N≡Ri(mod ai)(i=1,2,…,n)。

寻找一组数ki满足

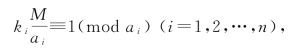
这里M=a1·a2·…·an。

令

，给定一次同余式的最小正整数解为

N=(R1k1G1+R2k2G2+…+RnknGn)-p M,

这里p为整数。

Bicker Paul提出过一个证明，现录如下：

因为a1，a2，…，an两两互素，衍母M=a1·a2·…·an，且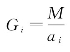，有（G1，a1）=（G2，a2）=…=（Gn，an）=1。

把k1G1+k2G2+…+knGn记作S。由k1G1≡1（mod ai），i=1，2，…，n，有

S≡k1G1≡1(mod a1),S-1≡0(mod a1),

S≡k2G2≡1(mod a2),S-1≡0(mod a2),

…,　…,

S≡knGn≡1(mod an),S-1≡0(mod an)。

这就表明S-1是a1，a2，…，an的倍数，M=a1·a2·…·an，因此S-1是a1·a2·…·an的倍数，即有

S-1≡0（mod M）或S≡1（mod M）。

因而，有

k1G1+k2G2+…+knGn≡1(mod M)。