从培养学生思维角度进行微课程教学设计
1.抽象思维能力：数学是人类思维的产物，具有高度的抽象性，虚数单位
、∞复数、扩充复平面等都是人类思维的自由创造，只能在大脑中想象，体现了数学具有高度的抽象性。
2.形象思维能力：
复数的几何意义：复数z=x+iy的模
是指复平面上的点z到原点的距离，复数可以由复平面上的点、向量、复球面等几何表示，形象直观，共轭复数具有鲜明的几何意义，复数的乘法z = z1z2的几何意义为：将z1的模|z1 |伸缩|z2|倍，再将其辐角按逆时针方向旋转Argz2，即先做一个相似变换，在做一个旋转变换。
几何上表示以原点为中心，
为半径的圆的内接正n边形的n个顶点。
3.类比思维能力：
复变函数是实数域上的微积分，和数学分析内容几乎相似，但由于复变函数的定义域和值域都是二维平面，所以它必定与实变量函数的性质有所差异，因此，在教学实践中所进行的微课程的教学设计都是从与实变量函数的联系与区别中进行，这样既有助于学生接受复变函数的新知识，又可以加深对数学分析知识的理解，做到知识的承前启后的效果，从而使学生的学习境界达到一定的高度，即在复变函数的学习中一定要善于运用类比的思维方法，要着眼于全局，掌握共性，留心特性，从推广、保留、失去、增加的角度研究复数的有关问题。如复数保留了实数的四则运算及运算规律（交换律、结合律、分配律），失去了实数的有序性，对于复数i，显然i≠ 0，假设i＞0，不等式两端同乘i，有i2＞0i，即-1＞0，与i＜0矛盾同理可得到与实数其他四则运算规律的矛盾性证明，即复数不能比较大小。
由复数定义知
，说明负数可以开偶次方，能开方的数的范围增加了。
复数的运算与向量运算类比，相同运算有“加”“减”“数乘”。向量是指自由向量（平移：左右、上下不变），复数以向量的形式进行平移仍然不变，旋转改变。不同点上复数有乘除、乘方、开方运算，向量没有，向量有数量积、向量积、混合积，复数没有。
4.创新思维能力：柯西积分公式的得到过程是创新思维过程。
由cauchy积分定理：若f（z）在单连通区域B上解析，c为B内简单闭曲线，则
=0（可理解为积分与路径无关，沿封闭曲线积分为零）。
条件可以放宽：设c为B的边界，若f（z）在单连通区域B内解析，在
=B+c上连续，则
.若z0为c内部的点，函数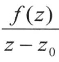
在c的内部不解析，则
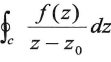不一定为零。那么应等于多少？由复合闭路定理知：
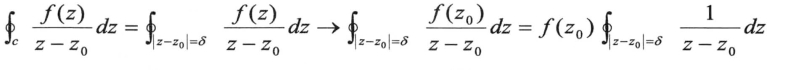
，得柯西积分公式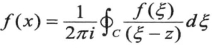
。此公式实质说明了一个解析函数f（z）是可以用积分来表示的，即在区域内任意点处的值，可以用其在边界上的积分来表示，解析函数f（z）的函数值之间是有密切联系的。