从知识实际应用背景的角度进行微课程教学设计
教学设计要渗透教学内容的应用价值，使学生认识到所学到知识是有用的，有利于调动学生学习的积极性和学习的兴趣。建立了复数概念，它是有其现实意义的，可以表示平面上的点，或向量，如普通照相机照出来的照片没有立体感。而数码相机照出来的照片有立体感，原因是普通照相机只是反映复数的距离（模），而数码相机除了反映模之外，还反映出每个点的位置（辐角），从而有了立体感。在信号处理时，复数的模|z|表示信号的幅度，辐角arg z表示给定频率的正弦波的相位。
调和函数是定义在实平面上的二元连续函数，具有二阶连续的偏导数，且满足拉普拉斯方程，如果只从数学的角度给出调和函数的定义，学生不仅意识不到它的重要性，而且会提出许多问题：偏微分方程的形式千千万万，这只算其中一种，为什么对这种方程进行讨论呢？
事实上，这个方程有着鲜明的理论背景，是从众多现象中抽象出来的，如在场论的研究中，我们设矢量场A为调和场，按定义rotA = 0，则存在u函数满足A = gradu，又divA=0，所以div（gradu）= 0。在直角坐标系中，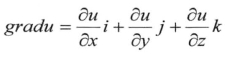
，所以有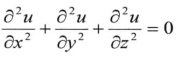
，此方程称为拉普拉斯方程。
在复变函数教学中运用微课程，一方面帮助教师突破教学中的困难，另一方面促进学生学习能力提高，同时改善了复变函数教学的现状，弥补了传统课堂教学模式的不足，即弥补了传统复变函数课堂教学不直观、不形象生动以及课前、课中、课后互动教学和个别辅导不足的缺点，使课堂教学变成有意义的活动，课堂效果得到了极大的提高，凸显了学生学习的主体地位，增强了学生学习的兴趣与效率。
参考文献
［1］钟玉泉复变函数论［M］高等教育出版社，北京，2013.
［2］李明泉工科复变函数课程教学改革探索与实践［J］武汉工程职业技术学院，2016，28（1）：104—105.
［3］张武威等微课程与翻转课堂相结合的教学方法创新应用［J］课程·教材·教法，2014，34（7）：10—16.
［4］李小刚等微型学习视野下的微课程设计及教学应用研究［J］现代教育技术，2013，23（10）：31—35.
【注释】
[1]基金项目：天津市十三五教育科学规划重点课题：微课程的大学数学翻转课堂教学模式的研究与实践（HE1020）。