从挖掘与渗透数学思想方法角度进行微课程教学设计
在教学过程中，以知识为载体，深入挖掘隐藏知识背后的思想方法，使学生用掌握的方法分析问题、解决问题。
1.一一对应的思想：复数不论是哪种表示法，都表现出复数与有序实数对一一对应的思想，如复数的代数z=x+iy形式和向量O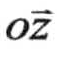
形式都与有序实数对（x，y）一一对应，复数的三角和指数形式即z = r（cosθ+isinθ）和z=reiθ均与有序实数对（r，9）一一对应，复数集与复平面上的点组成的集合之间建立了一一对应，复球面上的点与扩充复平面一一对应。
2.转化的思想：复数的几种表示法可以相互转化，如在对复数做乘法或开方运算时，需要将代数形式转化为三角形式或指数形式。由于复变量函数w = f（z）=u（x ，y）+ v（x ，y）与两个实的二元函数（u（x ，y），v（x y）一一对应，在研究复变量函数的极限、连续、可导（可微）、积分、级数时，均要转化为实变量的二元函数来讨论。
3.类比的思想：类比的思想方法自始自终贯穿在教学中，从保留、失去、增加的角度考察其与实变量函数的异同，指出复变量函数优于实变量函数的特性，引导学生在学习中既要找出共同点，更要弄清不同点，有利于学生深刻理解、灵活掌握复变量函数的理论和方法。
（1）复数与实数进行类比：复数z=x+iy，当虚部为零时转化为实数，是实数的推广，实数是复数的特例，复数不能比较大小，因此，实数中与“不等”有关的概念都不存在了，如复数没有正负可言，没有不等式，不考虑复变量函数的单调性、凹凸性、拐点、极最值，微分中值定理不再成立等。复数的加、减、乘、除、乘方、开方运算类比实数相应的运算。类比实数，既然复数可以看成点，则|z1-z2|表示复平面上两点的距离。
（2）复变量函数与实变量函数进行类比：从定义、符号表示、几何意义、运算、常见函数、极限、连续、导数、微分、积分、级数都进行类比。
如关于基本初等函数进行类比：复指数函数w=ez与实指数函数y=ex相同点在整个定义域上可导（解析），且导数为自身，即（ez）′=ez，并具有性质ez1 +z2 = ez1·ez2，由于y = ex定义域为（-∞ ，+∞），w=ez定义域为整个复平面，显然，y=ex为w=ez的特殊情况，而w=ez是y=ex的推广，w=ez不再具有单调性，且ez不再有乘幂的含义，极限
不存在，由指数函数定义ez+2kπi = ez ，w=ez为周期函数，基本周期为T=2πi，若ez1=ez2，则z1 = z2 + 2kπi，k∈Z。
（3）复变量函数可导与解析类比：复变量函数在z0点及邻域内可导，就称为在该点解析。从定义可以概括为“解析”为局部可导性，即f（z）在一点解析是指在一点及邻域可导，解析是可导的充分条件，可导不一定解析，不可导一定不解析，可导是解析的必要条件。一个解析函数在单连通区域D可导与解析等价。
（4）复变量函数展开成泰勒级数的形式与实变量函数完全相同，如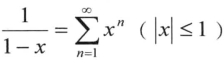
，
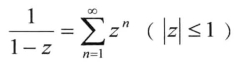，级数的绝对收敛与条件收敛的概念完全一致，因此，复变量函数的学习要完全类比实变量函数，同时掌握用已知解决未知的思想方法。
4.分类的思想：复数的实质是一种“有方向的数”，即“数量加方向”，其方向就是辐角的概念，当z=0时，辐角Argz不确定；当z≠0时，Argz = arg z + 2kπ，k∈Z，复变量函数的有限孤立奇点分为可去奇点、m级极点和本性奇点，都需要进行分类讨论。
5.推广的思想：由实数到复数就是推广思想的体现，复数的加法满足交换律与结合律，将两个复数加法运算推广到有限个复数相加，两个复数的乘法运算推广到有限个复数相乘，当有限个复数相同时，得到乘幂运算。