（一）模型应用

（一）模型应用

现假设有甲、乙、丙三个专业实训基地，现用本文所提的评价指标体系来对他们进行考核，考评的评语分为五级，评语集V=（优秀，良好，中等，合格，不合格），现有九位评审专家用Delphi法确定了各个指标的权重和评语集的权重，W=｛2，1，0，-1，-2｝，各指标的权重如下表1。

表1　评价指标及权重

表2　甲、乙、丙三个专业实训基地的基本评价信息表

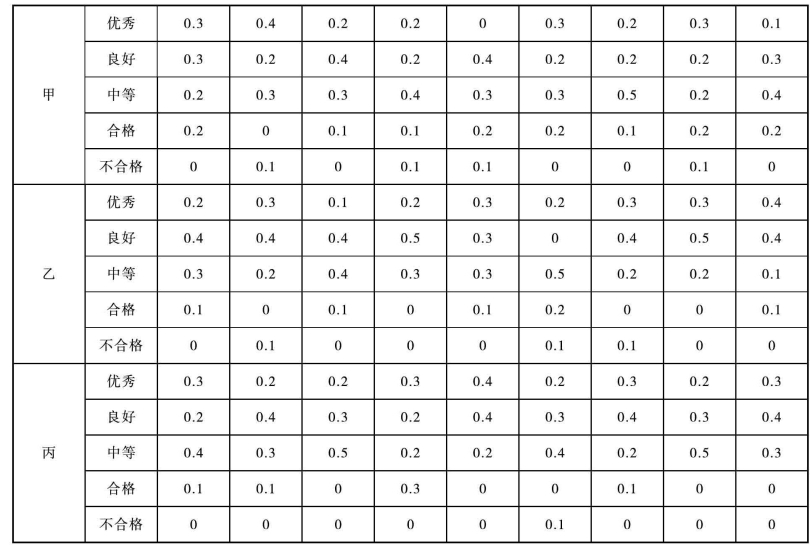
表2中甲的第一行值表示9位专家中有3位专家认为甲的设施设备优秀，3位专家认为为良好，2位专家认为合格，2位专家认为合格，1位专家认为不合格，其他数据以此类推。

现在我们以甲为例对第一个指标（设施设备）下的三个二级指标进行评价

同理可计算甲在第二个指标，第三个指标下的综合评价结果：

B2甲=A2·R2甲=（0.1，0.3，0.35，0.15，0.1），B3甲=A3·R3甲（0.24，0.22，0.33，0.18，0.03）

再回到一级指标，用此办法计算出甲的一级指标评价结果：

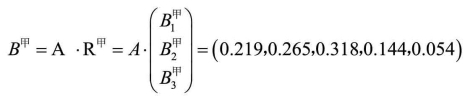
同理计算可得：

B乙=A·R乙=（0.254，0.364，0.285，0.065，0.032），B丙=A·R丙=（0.24，0.34，0.37，0.002，0.03）

最后，再用评语集的权重可以计算出甲、乙、丙三个专业实训基地的模糊综合评价得分值：

T甲=B甲·（2，1，0，-1，-2）T=0.451，

T乙=B乙·（2，1，0，-1，-2）T=0.743，

T丙=B丙·（2，1，0，-1，-2）T=0.741。

由于T乙＞T丙＞T甲，故而，就得分而言，乙最高，故而，在专业实训基地选择、建设时应将乙视为首选，因其模糊综合评分最高。